機械学習の分野では、バギング(bagging)というアンサンブル学習の方法があります。
なぜバギングは予測誤差を下げるのか?という点について少し学んだのでメモしておきます。
2日ほどはてなブログでの数式の記述(はてなTeX記法やMathJaxの手動導入など)と格闘しましたが、ある程度複雑な数式になるとどうしても表示が崩れてしまうので、諦めてgithub pagesに載せました
はてなブログには要点だけ載せます。 本来の記事全文は以下で御覧ください。
バギングによるバリアンスの低減
解析のため、非現実的な仮定を置きます。真の分布\(\mathcal P\)から無限に学習データセットが得られるとし、その下で構成される理想的な平均化推定量(aggregated estimator)\(\bar{f}(x) = \text{E}_{\mathcal P} [\hat{f}(x)]\)があったとします。
ここで\(\hat{f}(x)\)は分布\(\mathcal{P}\)から独立に取り出した学習データ\(\{x_i, y_i\}_{i=1}^N\)で学習した予測器の、入力点\(x\)における予測値です。
固定された入力点\(x\)の下での平均2乗誤差(MSE)を分解すると \[ \begin{align}\text{E}_{\mathcal P} [(Y - \hat{f}(x))^2]&= \text{E}_{\mathcal P} [(Y - \bar{f}(x) + \bar{f}(x) -\hat{f}(x))^2]\\ &= \text{E}_{\mathcal P} [(Y - \bar{f}(x))^2] + \underbrace{\text{E}_{\mathcal P} [(\hat{f}(x) - \bar{f}(x))^2]}_{Variance}\\ &\geq \text{E}_{\mathcal P} [(Y - \bar{f}(x))^2]\end{align} \] 2行目の第2項\(\text{E}_{\mathcal P} [(\hat{f}(x) - \bar{f}(x))^2]\)は平均\(\bar{f}(x)\)のまわりでの\(\hat{f}(x)\)の分散(バリアンス)です。
上の式は、\(Y\)と平均化推定量\(\bar{f}(x)\)の平均2乗誤差\(\text{E}_{\mathcal P} [(Y - \bar{f}(x))^2]\)は、\(Y\)と推定量\(\hat{f}(x)\)の平均2乗誤差\(\text{E}_{\mathcal P} [(Y - \hat{f}(x))^2]\)よりもバリアンスの分だけ小さいことを示しています。
一般的に、バイアスとバリアンスの間にはトレードオフ関係があり、バリアンスを下げるとバイアスが増える傾向がありますが、バギングを使うことで、バイアスを増やさずにバリアンスをゼロにすることができるわけです。
上の議論は真の分布\(\mathcal P\)から無限にデータセットが得られる場合で、現実にはありえません。Breiman (1996)が提案したバギングでは、この無限のデータセットをブートストラップサンプルで近似したものになります。ブートストラップによる現実のバギングでも、多くの場合はこのようにバリアンスを下げてくれます。
ただし、回帰においてバギングは平均2乗誤差を増加させず減少させますが、分類の場合は多数決になるので、一定以上の精度がないと逆に悪化させる可能性があります。
バギングの効果
Breiman(1999)が行った実験結果をまとめたのが以下の表です。
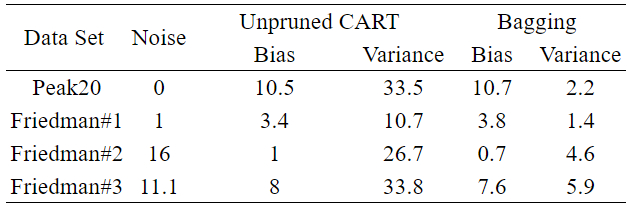
Data Setはデータセット名、Noiseはデータセットのノイズです。
Unpruned CARTは、枝刈りを行わなかった単体の決定木で、Baggingは枝刈りしていない50本の決定木で構成されたBaggingです。
理論解析の結論とほぼ合致していて、Baggingが単体の決定木と同程度のBiasを保ったままVarianceを大幅に削減していることがわかります。
理論解析と違ってVarianceがゼロにならないのは、
という理由が考えられます。
そのため、ランダムフォレスト(Breiman 2001)では、複数の決定木を作っていくフェーズで、あらかじめ決めた数の特徴量をランダムに選び出して決定木を作ることで決定木間の相関を大幅に減らすように工夫されています。
参考
Breiman, L. (1996). Bagging predictors. Machine learning, 24(2), 123-140.
Breiman, L. (2001). Random forests. Machine learning, 45(1), 5-32.
Hastie, T., Tibshirani, R., & Friedman, J. (2009). The elements of statistical learning: data mining, inference, and prediction. Springer Science & Business Media.