ドラッグしたりズームできるようなマップ上に散布図などを描きたいとき、FoliumだけでなくPlotlyも使えることを知ったのでメモしておきます。
環境
python:3.11のDocker Imageの下で、以下のバージョンのライブラリで試しました。
jupyterlab==4.0.10
plotly==5.18.0
pandas==2.1.4
以前のPlotlyはJupyterLabで使うとうまく表示されなくて、jupyter extensionや別のライブラリを追加したりといろいろ対策する必要があった記憶があるのですが、上記のバージョンでは何もせずとも問題なく描画できました。
データの用意
とりあえずいくつか点をplotできればいいので適当にマンションのデータを作ってみます。
import pandas as pd
df = pd.DataFrame([
dict(name="麻布台ヒルズ ガーデンプラザレジデンス", address="東京都港区虎ノ門5-9-1", lat=35.662242, lon=139.742654, price=900_000, size=80),
dict(name="六本木ヒルズレジデンス A棟", address="東京都港区六本木6丁目12-1", lat=35.658884, lon=139.728583, price=600_000, size=60),
dict(name="六本木ヒルズレジデンス B棟", address="東京都港区六本木6丁目12-2", lat=35.658869, lon=139.729598, price=650_000, size=65),
dict(name="六本木ヒルズレジデンス C棟", address="東京都港区六本木6丁目12-3", lat=35.658783, lon=139.730071, price=860_000, size=80),
dict(name="六本木ヒルズレジデンス D棟", address="東京都港区六本木6丁目12-4", lat=35.658901, lon=139.731209, price=400_000, size=80),
dict(name="六本木さくら坂レジデンス", address="東京都港区六本木6丁目16-6", lat=35.658113, lon=139.729766, price=1_700_000, size=200),
dict(name="元麻布ヒルズ", address="東京都港区元麻布1丁目3-1", lat=35.653843, lon=139.731913, price=750_000, size=80),
]).assign(
price_per_size = lambda self: (self.price / self.size).round(1)
)
緯度経度の情報がある手頃なデータが思いつかなかったので、MORI LIVINGさんのマンションからいくつか選び出し、Geocodingさんで住所を緯度経度に変換しました。
色の塗り分け用にそれっぽい価格もつけました。価格はモダンスタンダードさんの参考賃料を参考にそれっぽい値を入れています。
描いてみる
plotly.express.scatter_mapbox()で描くことができるようです
デフォルトだとMapBoxのAPIトークンが必要になりますが、mapbox_style='open-street-map'にすればトークンは不要です。
import plotly.express as px
fig = px.scatter_mapbox(
df,
lat="lat", lon="lon",
zoom=14, height=300,
hover_name="name",
hover_data=["name", "address", "price", "size"],
color = "price_per_size",
color_continuous_scale=px.colors.sequential.Blues[5:],
)
fig.update_layout(mapbox_style='open-street-map')
fig.update_layout(margin={"r":0,"t":0,"l":0,"b":0})
fig.show()

ただ、これだと地図の情報が多すぎて散布図が見づらい…。別のスタイルも試してみます。
carto-positronと carto-darkmatter の2つはかなりシンプルで、特にcarto-positronは見やすくていい感じでした。
import plotly.express as px
styles = ['carto-positron', 'carto-darkmatter']
for style in styles:
print(f"mapbox_style={style}")
fig = px.scatter_mapbox(
df,
lat="lat", lon="lon",
zoom=14, height=300,
hover_name="name",
hover_data=["name", "address", "price", "size"],
color = "price_per_size",
color_continuous_scale=px.colors.sequential.Blues[5:],
)
fig.update_layout(mapbox_style=style)
fig.update_layout(margin={"r":0,"t":0,"l":0,"b":0})
fig.show()

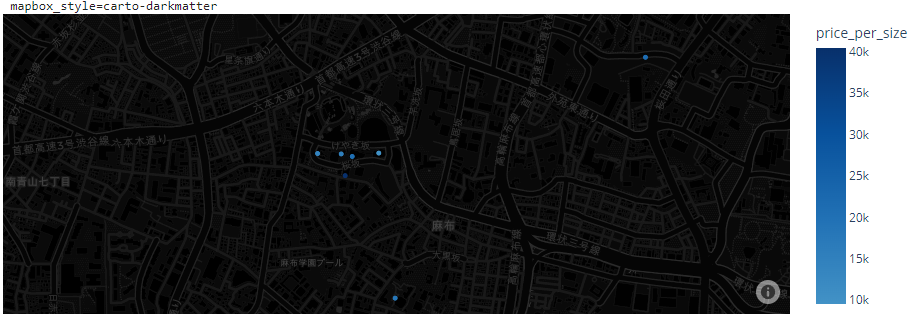
自由にズームしたり、ホバーしたときに他の変数の値も見られるようにできるので、データの確認をするのに良さそうな感じです。

Rを使っていたときはplotlyをよく使っていたのですが、Pythonではまだまだ使いこなせてないので(Dashとかも)、この本も参考にしつつ勉強してみようかとおもいます(Plotlyを深く解説してるほぼ唯一の本)。