LOWESS (locally weighted scatterplot smoothing) は散布図に対して下記のような近似曲線を描いてくれる便利な手法です。

statsmodelsパッケージだと

import statsmodels.api as sm
smoothed = sm.nonparametric.lowess(exog=x, endog=y, frac=0.5, it=3)

といった感じで気軽に実行できますが、frac（使用するサンプルの割合）やit（繰り返し数）といったハイパーパラメータがどう作用するのかについては、アルゴリズムを知らないとよくわからずモヤッとしたので調べてみました。

今回はLOWESSが提案されたとされる論文

Cleveland, W. S. (1979). Robust locally weighted regression and smoothing scatterplots. Journal of the American statistical association, 74(368), 829-836.

を読んだので、アルゴリズムとPythonでの実装例をメモしておきます。

LOWESSのアルゴリズム
Pythonでの実装例

LOWESSのアルゴリズム

$i$ 番目のサンプルの目的変数 $y_i$ を特徴量 $x_i$ とノンパラメトリックの平滑化関数 $g(x_i)$ で近似することを考えます。

$\displaystyle y_i = g(x_i) + \epsilon_i$

ここで $\epsilon_i$ は平均0で分散が一定の確率変数です。

重みの計算と $r$ 個の最近傍サンプルの取得

$x_i$ について、 $j=1,\dots,n$ にわたって $|x_i - x_j|$ で距離を測り、 $r$ 番目に近いサンプルとの距離を $h_i$ とします。

重み関数 $W(\cdot)$ を用いて、 $k=1,\dots,n$ について

$\displaystyle w_k(x_i) = W(h_i^{-1}(x_k - x_i))$

を計算します。

ここで重み関数 $W(\cdot)$ は以下の性質を満たすものとします。

$|x| \lt 1$ について $W(x) > 0$
$W(-x)=W(x)$
$W(x)$ は $x \geq 0$ について非増加関数
$|x| \geq 1$ について $W(x)=0$

論文では $W$ の例として tricube function が使われています（ちなみに、Wikipediaではもっと新しいやり方としてGaussian functionを使う方法が書いてありました：Local regression - Wikipedia）

$\displaystyle W(x) = \begin{cases} (1-|x|^3)^3 & \text { for } \quad|x|<1 \\ 0 \quad & \text { for } \quad|x| \geqslant 1 \end{cases}$

これはグラフを描くと次の図のようになる関数です。

$h_i^{-1}(x_k - x_i)$ は分子の $x_k - x_i$ の絶対値が分母の $h_i$ より大きければ $|h_i^{-1}(x_k - x_i)| \geq 1$ になるので重みが0になります。つまり、サンプルとして回帰に使用されなくなります。なので重み関数は $i$ 番目のサンプルの近傍の $r$ 個のサンプルを取り出しつつ、 $r$ 個のサンプルにも距離に応じた重みをかけているわけです。

statsmodelsのlowessのパラメータ「frac（使用するサンプルの割合）」は、この $r$ の計算に使われているものと思われます。

多項式回帰のフィッティング

非線形回帰として $d$ 次の多項式回帰を行います。

$\displaystyle \min_{\beta_0,\dots,\beta_d} ~ \sum_{k=1}^n w_k\left(x_i\right)\left(y_k-\beta_0-\beta_1 x_k-\ldots-\beta_d x_k^d\right)^2$

$\displaystyle \hat{y}_i=\sum_{j=0}^d \hat{\beta}_j\left(x_i\right) x_i^j$

ロバスト性重み $\delta$ の計算

続いて、外れ値の影響を除外するための重みを計算します。次のように定義される bisquare weight function $B(x)$ を用います。

$\displaystyle B(x) = \begin{cases} (1 - x^2)^2 & \text { for } \quad|x| < 1 \\ 0 \quad & \text { for } \quad|x| \geqslant 1 \end{cases}$

残差 $e_i = y_i - \hat{y}_i$ の絶対値 $|e_i|$ の中央値を $s$ とします。ロバスト性重み（robustness weights）を

$\displaystyle \delta_k = B(e_k / 6s)$

と定義します。 $B(x)$ もtricube functionと似た形状であり、残差の絶対値の中央値の6倍（ $6s$ ）以上の絶対値の残差 $|e_k/6s| \geq 1$ を持つ外れ値は重み $\delta_k$ がゼロになり、推定に含まれなくなるので推定が外れ値の影響を受けなくなります。

$\delta$ を使って重み付け回帰を行う

$\delta_k w_k (x_i)$ を重みとして再び $d$ 次多項式回帰を行い、新たな推定値 $\hat{y}_i$ を得ます。

繰り返す

ロバスト性重み $\delta$ の計算
$\delta$ を使って重み付け回帰を行う

のステップを $t$ 回繰り返します。

Pythonでの実装例

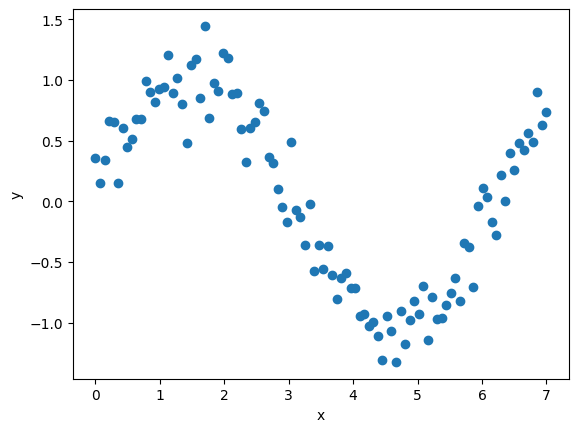
例として、次のデータを使います

# サンプルデータ
import numpy as np
n = 100
np.random.seed(0)
x = np.linspace(0, 7, n)
y = np.sin(x) + np.random.normal(0, 0.2, n)

図にするとこんな感じです。

重み関数を定義しておきます

def tricube(x: np.array) -> np.array:
    w = (1 - np.abs(x)**3)**3
    w[np.abs(x) >= 1] = 0
    return w

def bisquare(x: np.array) -> np.array:
    w = (1 - np.abs(x)**2)**2
    w[np.abs(x) >= 1] = 0
    return w

ハイパーパラメータを定義してLOWESSを推定します

# ハイパーパラメータの定義
frac = 0.66 # 使用するサンプルの割合
r = int(frac * n)  # 使用する近傍のサンプル数
d = 3  # 多項式回帰の次数
t = 3  # iteration

# 前処理：d次多項式を作るための特徴量生成
X = np.vstack([x**j for j in range(d)]).T

# LOWESSの推定
n = X.shape[0]
delta = np.ones_like(x)
y_pred = np.zeros_like(x)
for _ in range(t):
    for i in range(n):
        # 重みの計算
        dist = x - x[i]
        idx = np.argsort(np.abs(dist))[:r]
        h_i = np.abs(dist[idx]).max() # r番目に近いdiff
        w = tricube(dist / h_i)
        W = np.diag(delta * w)

        # WLS
        beta = np.linalg.inv(X.T @ W @ X) @ X.T @ W @ y
        y_pred[i] = X[i,:] @ beta

    e = y - y_pred
    s = np.median(np.abs(e))
    delta = bisquare(e / (6 * s))