「自分で数式をコードに落としていって動かす」という作業は非常に勉強になると思ったので,いろんなアルゴリズムをゼロから作っていくことで勉強してみたいと思います。
今回は最尤推定とロジスティック回帰についてです。最尤法のほうはおまけで,ロジスティック回帰がメインです。
恥ずかしながら,ロジスティック回帰モデルについては「パラメータ推定に最尤法を使うらしい」くらいしか理解しておらず,今回はじめて真面目に勉強しました…。
記事の前半で理論の要点を整理して,後半でコードを動かしていく構成になります。
最尤推定法
まず,ロジスティック回帰でも使う推定方法について。
尤度
例えば,次のような問題について考えてみます。
あるコインを5回投げて2回が表になった。
このコインを投げたときに表が出る確率は?
この「表が出る確率」が推定したいパラメータになります。
表(head)が出ることを\(h=1\),裏が出ることを\(h = 0\)とし,\(h = 1\)となる確率を\(\theta\),\(h=0\)となる確率を\((1-\theta)\)とします。 \[ h = \begin{cases} 0 & \text{コインが裏のとき}\\ 1 & \text{コインが表のとき} \end{cases} \\ P(h = 1) = \theta, \hspace{2em} P(h=0) = (1-\theta) \] コインを5回投げて2回が表になる確率は,2項分布に従うと考えれば\({}_n\mathrm{C}_kp^k(1-p)^{n-k}\)なので
\[ P(h = {0, 0, 0, 1, 1}) = {}_{5}\mathrm{C}_{2} \theta^2 (1-\theta)^3 \]
となります。
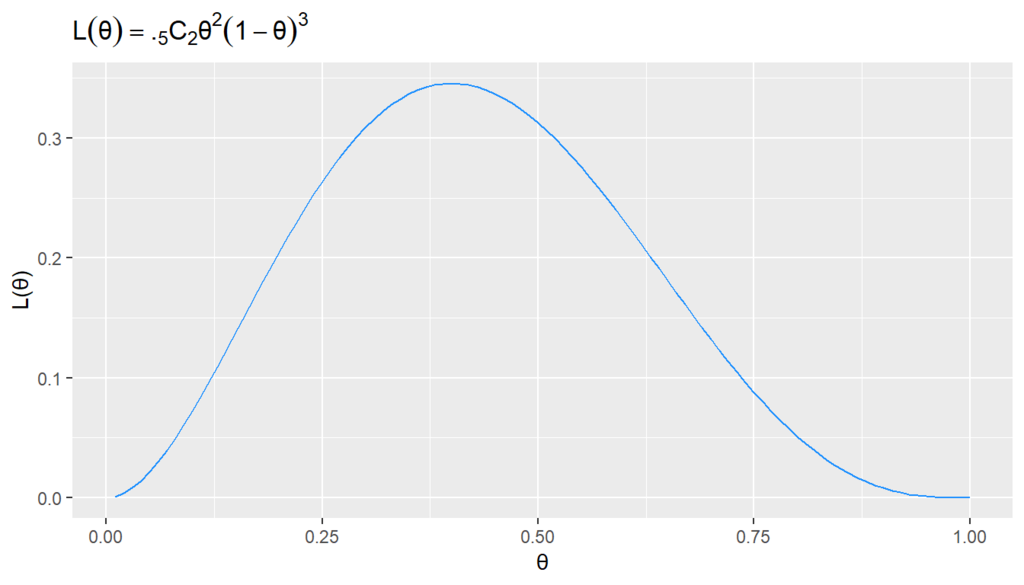
この確率を尤度(ゆうど,likelihood)と呼び,多くの場合\(L(\theta)\)のように表記されます。 \[ L(\theta) = {}_{5}\mathrm{C}_{2} \theta^2 (1-\theta)^3 \] 尤度が最大になるパラメータ\(\theta\)が「最も尤もらしい(もっともらしい)」パラメータであるというわけです。
この尤度関数を描いてみると,0.4のあたりで最大になっていることが目視でもわかります。
library(tidyverse) # 尤度関数 likelihood = function(θ, n = 5, k = 2){ choose(n, k) * θ^k * (1 - θ)^(n-k) # nCk p^k (1-p)^{n-k} } # 描画用データ θ = 1:100 * 0.01 L = likelihood(θ) df = data_frame(θ, L) # plot ggplot(df, aes(x = θ, y = L))+ geom_line(color = "dodgerblue")+ labs(y = "L(θ)", title = expression(L(θ)==.[5]*C[2] * θ^2 * (1 - θ)^3))
対数尤度
尤度\(L(\theta)\)を最大にする\(\theta\)と対数尤度\(\log L(\theta)\)を最大にする\(\theta\)は同じなので,対数尤度を最大にする方法でも推定できます。
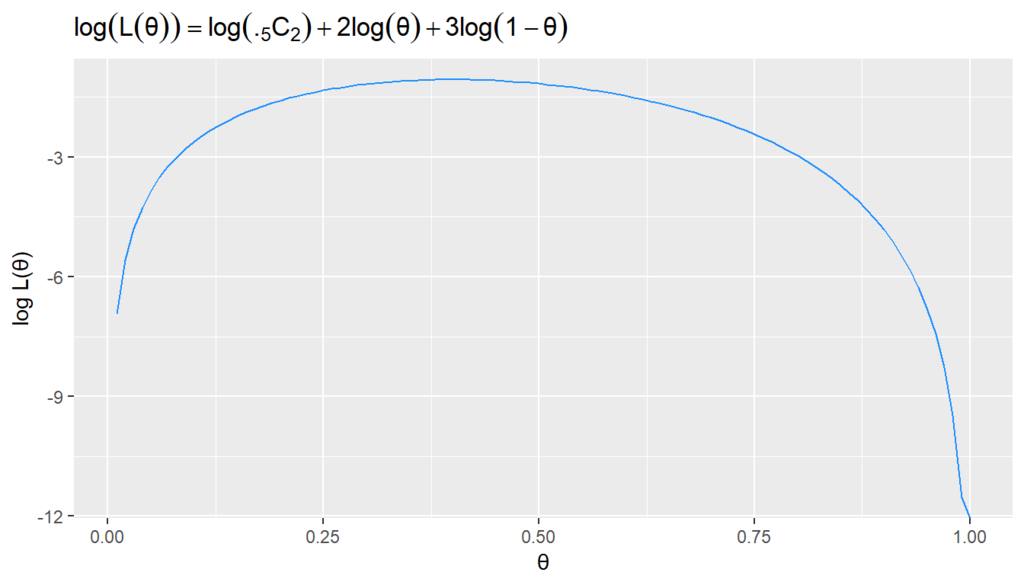
尤度は確率を沢山掛け合わせたものになって非常に小さな値を扱うことになりますが,対数尤度では対数にすることによって掛け算が足し算になります1。そのため,最尤推定では計算を簡単にするために対数尤度(log likelihood)が使われます。 \[ \begin{align} \log L(\theta) &= \log\{{}_{5}\mathrm{C}_{2} \theta^2 (1-\theta)^3\} \\ &= \log{}_{5}\mathrm{C}_{2} + 2\log \theta + 3\log (1-\theta)\\ \end{align} \]
df = data_frame(θ, logL=log(L)) # plot ggplot(df, aes(x = θ, y = logL))+ geom_line(color = "dodgerblue")+ labs(y = "log L(θ)", title = expression(log(L(θ))==log(.[5]*C[2]) + 2*log(θ) + 3 * log(1 - θ)))
これをパラメータ\(\theta\)で微分すると, \[ \begin{align} \frac{d \log L(\theta)}{d \theta} &= 2 \cdot \frac{1}{\theta} + 3 \cdot \frac{1}{1-\theta} \cdot (-1)\\ &= \frac{2}{\theta} - \frac{3}{1 - \theta} \end{align} \]
# 微分 logL = expression(log(c) + 2 * log(t) + 3 * log(1-t)) D(logL, "t")
> D(logL, "t") 2 * (1/t) - 3 * (1/(1 - t))
\(\log L(\theta)\)を最大にするパラメータ\(\theta^*\)は, \[ \frac{d \log L(\theta)}{d \theta} = \frac{2}{\theta} - \frac{3}{1 - \theta} = 0 \] となる\(\theta\)なので, \[ \theta^* = \frac{2}{5} = 0.4 \] となります。
このように尤度を最大にするパラメータを点推定する方法が最尤推定法になります。
ロジスティック回帰
シグモイド関数
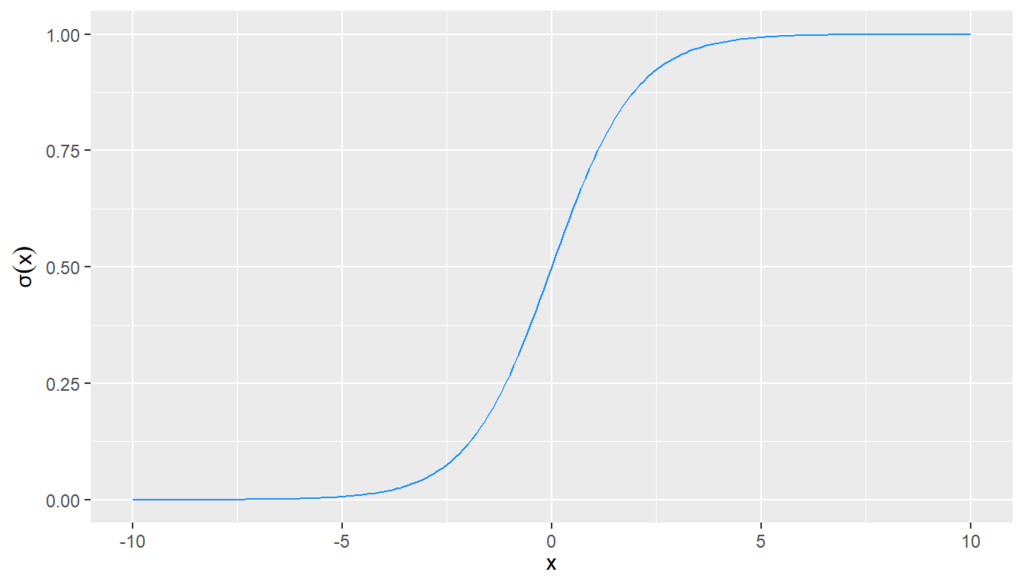
シグモイド関数(sigmoid function)は無限区間\((-\infty, \infty)\)の数を区間\((0,1)\)に変換する関数です2。ロジスティック関数(logistic function)とも呼ばれます 3。
ロジスティック回帰ではシグモイド関数を使うことで確率や二値変数を目的変数に使った回帰モデルを作ります。
# シグモイド関数 sigmoid = function(x) 1 / (1 + exp(-x)) # データ生成 x = -100:100 * 0.1 y = sigmoid(x) # plot ggplot(data_frame(x, y), aes(x = x, y = y))+ geom_line(color = "dodgerblue")+ labs(y = expression(σ(x)), x = expression(x))
ロジット関数
目的変数\(y\in \{0,1\}\)を\(p\)次元説明変数\(\boldsymbol{x}=(x_1,...,x_p)^T\)で説明することを考えます。
\(\boldsymbol{x}\)の下で\(y=1\)になる条件付き確率と\(y=0\)になる条件付き確率を \[ P(y=1|\boldsymbol{x}) = \pi(\boldsymbol{x}), \hspace{2em} P(y=0|\boldsymbol{x}) = 1-\pi(\boldsymbol{x}) \]
とするとき,その確率の比をオッズ(odds)といいます。 \[ \text{odds}(\pi(\boldsymbol{x})) = \frac{\pi(\boldsymbol{x})}{1-\pi(\boldsymbol{x})} \] オッズの対数は対数オッズ(log odds)やロジット関数(logit function)と呼ばれます。 \[ \text{logit}(\pi(\boldsymbol{x})) = \log{\frac{\pi(\boldsymbol{x})}{1-\pi(\boldsymbol{x})}} \]
ロジスティック回帰モデル
一般化線形モデルの文脈では,リンク関数にロジット関数を用いて目的変数\(y\)と線形予測子\(\beta_0 + \beta_1 x_{1} + \cdots + \beta_p x_{p}=\boldsymbol{\beta}^{\top}\boldsymbol{x}\)を繋げた \[ \log{\frac{\pi(\boldsymbol{x})}{1-\pi(\boldsymbol{x})}} = \beta_0 + \beta_1 x_{1} + \cdots + \beta_p x_{p}=\boldsymbol{\beta}^{\top}\boldsymbol{x} \] をロジスティック回帰モデルと呼ぶようです(本橋 2015)。
これの両辺の指数をとると \[ \frac{\pi(\boldsymbol{x})}{1-\pi(\boldsymbol{x})} = \exp(\boldsymbol{\beta}^{\top}\boldsymbol{x}) \] であり,整理すると4 \[ \pi(\boldsymbol{x}) =\frac{\exp(\boldsymbol{\beta}^{\top}\boldsymbol{x})}{1 + \exp(\boldsymbol{\beta}^{\top}\boldsymbol{x})} \] と,シグモイド関数になります。
\(P(y=1|\boldsymbol{x}) = \pi(\boldsymbol{x})\)でしたので,\(\boldsymbol{x}\)の下で\(y=1\)になる確率\(P(y=1|\boldsymbol{x})\)を目的変数にして,ロジスティック関数を介して線形予測子\(\boldsymbol{\beta}^{\top}\boldsymbol{x}\)で説明している・・という感じになるようです。 \[ P(y=1|\boldsymbol{x}) = \pi(\boldsymbol{x}) =\frac{\exp(\boldsymbol{\beta}^{\top}\boldsymbol{x})}{1 + \exp(\boldsymbol{\beta}^{\top}\boldsymbol{x})} \]
パラメータの推定
ここまでで「確率や二値変数をどう\(\boldsymbol{\beta}^{\top}\boldsymbol{x}\)で説明するか」が定まったので,次はパラメータの推定について整理します。
誤差関数
最小二乗法では誤差関数に誤差ニ乗和(Sum of Squared Error:SSE)や平均二乗誤差(Mean Squared Error:MSE)を使いましたが,ロジスティック回帰では交差エントロピー誤差関数(cross-entropy error function)を使います。
モデルの目的変数\(y\in\{0,1\}\)が1をとる確率と0をとる確率をそれぞれ \[ P(y=1) = \pi, \hspace{1em} P(y=0) = 1- \pi \] と書くことにします。また確率変数\(y\)はパラメータ\(\pi\)のベルヌーイ分布に従う(\(y \sim Bern(\pi)\))とし, \[ f(y|\pi)=\pi^{y} (1 - \pi)^{1-y} \] とします。
\(N\)回の試行に基づく尤度関数 \[ L(\pi_1,...,\pi_N) = \prod_{i=1}^N f(y_i|\pi_i) = \prod_{i=1}^N \pi_i^{y_i} (1 - \pi_i)^{1-y_i} \] の対数をとって負の符号を付けたもの \[ \begin{align} \mathcal{L}(\pi_1,...,\pi_N) &= - \log L(\pi_1,...,\pi_N)\\ &= -\sum_{i=1}^N \{y_i \log \pi_i + (1-y_i) \log(1-\pi_i)\} \end{align} \] が交差エントロピー誤差関数になります。
先程の \[ \pi_i = \frac{\exp(\boldsymbol{\beta}^{\top}\boldsymbol{x}_i)}{1 + \exp(\boldsymbol{\beta}^{\top}\boldsymbol{x}_i)} \] を代入して整理すれば, \[ \mathcal{L}(\pi_1,...,\pi_N) = \mathcal{L}(\boldsymbol{\beta}) = -\sum_{i=1}^N \{y_i \boldsymbol{\beta}^{\top}\boldsymbol{x}_i - \log (1 + \exp(\boldsymbol{\beta}^{\top}\boldsymbol{x}_i))\} \] になります(ただし,\(\boldsymbol{x}_i\)は入力ベクトル…レコード\(i\)の説明変数達です)
また,これの勾配(微分したもの)は \[ \frac{\partial \mathcal{L}(\boldsymbol{\beta})}{\partial \boldsymbol{\beta}} = -\sum_{i=1}^N \left\{y_i \boldsymbol{x}_i - \frac{\boldsymbol{x}_i\exp(\boldsymbol{\beta}^{\top}\boldsymbol{x}_i)}{1 + \exp(\boldsymbol{\beta}^{\top}\boldsymbol{x}_i)}\right\} = \sum_{i=1}^N \boldsymbol{x}_i (\pi_i - y_i) \] になります。
尤度関数・交差エントロピー誤差は最小二乗法のMSEなどとは異なり解析的に解が出せないので,勾配降下法やニュートン・ラフソン法を使って,コンピュータでゴリゴリと数値計算をして解を出します。
交差エントロピー誤差を\(N\)で割った平均交差エントロピー誤差関数 \[ -\frac{1}{N}\sum_{i=1}^N \{y_i \boldsymbol{\beta}^{\top}\boldsymbol{x}_i - \log (1 + \exp(\boldsymbol{\beta}^{\top}\boldsymbol{x}_i))\} \] というのもあるようです。こちらのほうが誤差がデータ数の影響を受けにくいのだとか(伊藤 2018)。
勾配降下法
勾配降下法(gradient descent method,あるいは最急降下法steepest descent method)5は
- 係数(重み)の初期値を決める
- 誤差を評価する
- 係数を誤差関数の勾配に基づいて更新する
- 2~3を繰り返す
という感じの方法です。
係数の更新には次の式が使われます。 ここでは学習率(learning rate)と呼ばれるもので,係数を更新するときに値を大きく変えすぎないように0.01とか小さな値を設定します。
Rで実装
irisデータセットのうちSpecies列が2値のデータを使います。
手元の本に具体的なアルゴリズムの例がないので一部想像で補完してコードを書きます(係数の初期値とか)。
# データ df = iris[51:150,] # 51 ~ 150行 X = cbind(Intercept = 1, df[,-5]) %>% as.matrix() # 切片項用の列を追加 y = ifelse(df[,5] == "versicolor", 0, 1) # versicolor = 0, virginica = 1 # シグモイド関数 sigmoid = function(x) exp(x) / (1 + exp(x)) # 勾配降下法の関数を定義 GradientDescent = function(X, y, K = 10, eta = 0.001) { # K:重み更新の反復回数, eta: 学習率 n = dim(X)[1] # サンプルサイズ p = dim(X)[2] # 説明変数の数 beta = runif(p) k = 1 # カウントをリセット while (k != K) { # 線形予測子Xβをシグモイド関数に通す pi = sigmoid(X %*% beta) # 交差エントロピー誤差関数の勾配 gradient = 0 # 初期化 for(i in 1:n){ # 総和 gradient = gradient + X[i,] * (pi[i] - y[i]) } # 係数の更新 ## β := β - eta * 誤差関数の勾配 beta = beta - eta * gradient # (係数の更新の様子を記録) ## 誤差 MSE = mean((pi - y)^2) ## データフレームにまとめる df_k = data.frame(k, t(beta), MSE) ## 結合 if(k == 1) df = df_k if(k != 1) df = rbind(df, df_k) # カウントを更新 k = 1 + k } # 結果 result = list(coefficients = beta, # データにフィットさせた係数 MSE = MSE, # 最終的なMSE log = df) # 係数の更新の様子 return(result) }
推定したパラメータは次のようになりました。
# パラメータの推定 result = GradientDescent(X, y, K = 20000) # 推定した係数 result$coefficients
## Intercept Sepal.Length Sepal.Width Petal.Length Petal.Width ## -7.597939 -4.262963 -4.924182 6.707644 9.197969
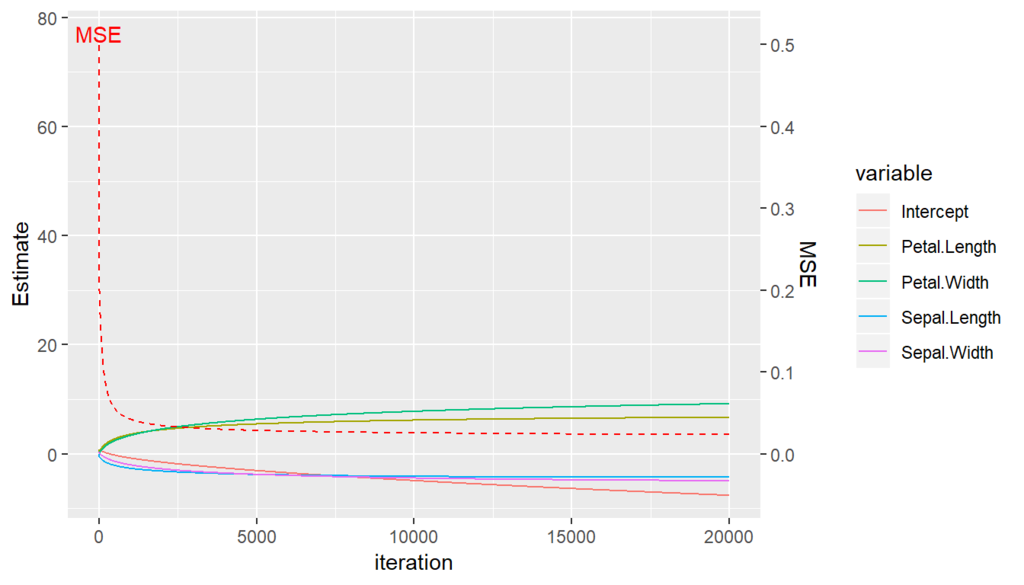
20000回の重みの更新とMSEの推移が次のグラフです。
20000回やってもまだ推定値が収束せず,反復回数を増やすたびにじわじわ動いていて,MSEもじわじわ動いているので,反復回数が足りないようです。
(MSEを予測精度の評価に使うのは雑な気がしますが,まぁ参考程度ということで…。)
# plot temp = result$log %>% gather(variable, value, 2:6) ggplot() + geom_line(aes(x = temp$k, y = temp$value, color = temp$variable))+ geom_line(aes(x = temp$k, y = temp$MSE * 150), color = "red", linetype = 2) + scale_y_continuous(sec.axis = sec_axis(~ . /150, name = "MSE")) + annotate("text", x = temp$k[1], y = temp$MSE[1] * 150 + 2, label = "MSE", color = "red")+ labs(y = "Estimate", x = "iteration", color = "variable")
最終的なMSEはこうなりました。
str_c("MSE: ", result$MSE) # MSE
## [1] "MSE: 0.0234984687192942"
ちなみに,ニュートン法を使用しているglm()とはだいぶ結果が違います…。
# glmと比較 res_glm = glm(Species ~ . , data = iris[51:150,], family = binomial(link = "logit")) res_glm
## ## Call: glm(formula = Species ~ ., family = binomial(link = "logit"), ## data = iris[51:150, ]) ## ## Coefficients: ## (Intercept) Sepal.Length Sepal.Width Petal.Length Petal.Width ## -42.638 -2.465 -6.681 9.429 18.286 ## ## Degrees of Freedom: 99 Total (i.e. Null); 95 Residual ## Null Deviance: 138.6 ## Residual Deviance: 11.9 AIC: 21.9
y_hat = res_glm$fitted.values str_c("glmのMSE: ",(y - y_hat)^2 %>% mean())
## [1] "glmのMSE: 0.0188203802832239"
glmのほうがMSEを小さくできていますね
ニュートン法
ニュートン法(Newton's method)あるいはニュートン・ラフソン法(Newton-Raphson method)は,誤差関数をテイラー展開で近似したものを使って解く方法です。
次のように係数(重み)\(\boldsymbol{\beta}\)を更新していきます。 \[ \boldsymbol{\beta}^{(new)} = \boldsymbol{\beta}^{(old)} - \boldsymbol{H}^{-1} \frac{\partial \mathcal{L}(\boldsymbol{\beta})}{\partial \boldsymbol{\beta}} \] ここで\(\boldsymbol{H}\)はヘッセ行列(Hessian matrix)という,\(\boldsymbol{\beta}\)の2次の導関数を要素に持つ行列で,その\((i,j)\)要素は \[ (\boldsymbol{H})_{ij} = \frac{\partial^2 \mathcal{L}(\boldsymbol{\beta})}{\partial \beta_i \partial \beta_j} \] つまり \[ \boldsymbol{H}= \left( \begin{array}{cccc} \frac{\partial^2 \mathcal{L}(\boldsymbol{\beta})}{\partial \beta_0^2} & \frac{\partial^2 \mathcal{L}(\boldsymbol{\beta})}{\partial \beta_0 \partial \beta_1} & \cdots & \frac{\partial^2 \mathcal{L}(\boldsymbol{\beta})}{\partial \beta_0 \partial \beta_p} \\ \frac{\partial^2 \mathcal{L}(\boldsymbol{\beta})}{\partial \beta_1 \partial \beta_0} & \frac{\partial^2 \mathcal{L}(\boldsymbol{\beta})}{\partial \beta_1^2} & \cdots & \frac{\partial^2 \mathcal{L}(\boldsymbol{\beta})}{\partial \beta_1 \partial \beta_p} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 \mathcal{L}(\boldsymbol{\beta})}{\partial \beta_p \partial \beta_0} & \frac{\partial^2 \mathcal{L}(\boldsymbol{\beta})}{\partial \beta_p \partial \beta_1} & \cdots & \frac{\partial^2 \mathcal{L}(\boldsymbol{\beta})}{\partial \beta_p^2} \end{array} \right) \] のような行列になります。
反復再重み付け最小二乗法(IRLS)
ニュートン・ラフソン法を交差エントロピー誤差関数に適用したものは反復再重み付け最小二乗法(iteratively reweighted least squares:IRLS)と呼ばれるようで,Rのglm.fit()でもそう呼ばれています。
The default method
"glm.fit"uses iteratively reweighted least squares (IWLS)
(glm function | R Documentationより)
ニュートン・ラフソン法を交差エントロピー誤差関数に適用する場合,ニュートン・ラフソン法のヘッセ行列は \[ \boldsymbol{H} = \frac{\partial^2 \mathcal{L}(\boldsymbol{\beta})}{\partial \boldsymbol{\beta} \partial \boldsymbol{\beta}^{\top}} = \sum_{i=1}^N \pi_i (1 - \pi_i) \boldsymbol{x}_i \boldsymbol{x}_i^{\top} = \boldsymbol{X}^{\top} \boldsymbol{W}\boldsymbol{X} \] になります。ここで\(\boldsymbol{X}\)はデータの行列で,\(\boldsymbol{W}\)は\(N\times N\)対角行列で,その要素は \[ W_{ii} = \pi_i(1 - \pi_i) \] になります。
そして,重みの更新は \[ \boldsymbol{\beta}^{(new)} = \boldsymbol{\beta}^{(old)} - (\boldsymbol{X}^{\top} \boldsymbol{W}\boldsymbol{X})^{-1} \frac{\partial \mathcal{L}(\boldsymbol{\beta})}{\partial \boldsymbol{\beta}} \] となり, \[ \frac{\partial \mathcal{L}(\boldsymbol{\beta})}{\partial \boldsymbol{\beta}} = \sum_{i=1}^N \boldsymbol{x}_i (\pi_i - y_i) = \boldsymbol{X}^{\top}(\boldsymbol{\pi} - \boldsymbol{y}) \] なので \[ \boldsymbol{\beta}^{(new)} = \boldsymbol{\beta}^{(old)} - (\boldsymbol{X}^{\top} \boldsymbol{W}\boldsymbol{X})^{-1} \boldsymbol{X}^{\top}(\boldsymbol{\pi} - \boldsymbol{y}) \] となります。
また, \[ \boldsymbol{z} = \boldsymbol{X} \boldsymbol{\beta} - \boldsymbol{W}^{-1}(\boldsymbol{\pi} - \boldsymbol{y}) \] とおけば \[ \begin{align} \boldsymbol{\beta}^{(new)} &= \boldsymbol{\beta}^{(old)} - (\boldsymbol{X}^{\top} \boldsymbol{W}\boldsymbol{X})^{-1} \boldsymbol{X}^{\top}(\boldsymbol{\pi} - \boldsymbol{y}) \\ &=(\boldsymbol{X}^{\top} \boldsymbol{W}\boldsymbol{X})^{-1} \{\boldsymbol{\beta} - \boldsymbol{X}^{\top}(\boldsymbol{\pi} - \boldsymbol{y})\}\\ &=(\boldsymbol{X}^{\top} \boldsymbol{W}\boldsymbol{X})^{-1} \boldsymbol{X}^{\top} \boldsymbol{W} \boldsymbol{z} \end{align} \] と書くこともできます(最終的に加重最小二乗法の正規方程式みたいな形になります)。
Rで実装
手元の本に具体的なアルゴリズムの例がないので一部想像で補完してコードを書きます。
試してみたところ,係数の初期値は乱数でも固定値でもよさそうですが,0.1とか微小な値にするのが良さそうです。0.7とかだと収束しない場合が…
# IRLS関数を定義 IRLS = function(X, y, K = 20) { # K:重みを更新する反復回数 n = dim(X)[1] # サンプルサイズ p = dim(X)[2] # 説明変数の数 # 係数βの初期値をランダムに決める beta = runif(n = p, max = 0.1) k = 1 # カウントをリセット while (k != K) { # 線形予測子Xβをシグモイド関数に通す pi = sigmoid(X %*% beta) # 重み行列 W の作成 W = matrix(0, ncol = n, nrow = n) # 値を入れるための空行列 for(i in 1:n) { W[i,i] = pi[i] * (1 - pi[i]) } # 係数の更新 ## β := β - (X'WX)^{-1}X'(pi-y) beta = beta - solve(t(X) %*% W %*% X) %*% t(X) %*% (pi - y) # (係数の更新の様子を記録) ## 誤差 MSE = mean((pi - y)^2) ## データフレームにまとめる df_k = data.frame(k, t(beta), MSE) ## 結合 if(k == 1) df = df_k if(k != 1) df = rbind(df, df_k) # カウントを更新 k = 1 + k } # 結果 result = list(coefficients = beta, # データにフィットさせた係数 MSE = MSE, # 最終的なMSE log = df) # 係数の更新の様子 return(result) }
20回の重みの更新を行うようにして推定したところ,推定したパラメータは次のようになりました。
# パラメータの推定 result = IRLS(X, y, K = 20) # 推定した係数 result$coefficients
## [,1] ## Intercept -42.637804 ## Sepal.Length -2.465220 ## Sepal.Width -6.680887 ## Petal.Length 9.429385 ## Petal.Width 18.286137
# glmと比較 glm(Species ~ . , data = iris[51:150,], family = binomial(link = "logit"))
## ## Call: glm(formula = Species ~ ., family = binomial(link = "logit"), ## data = iris[51:150, ]) ## ## Coefficients: ## (Intercept) Sepal.Length Sepal.Width Petal.Length Petal.Width ## -42.638 -2.465 -6.681 9.429 18.286 ## ## Degrees of Freedom: 99 Total (i.e. Null); 95 Residual ## Null Deviance: 138.6 ## Residual Deviance: 11.9 AIC: 21.9
IRLSで解いているglm()の係数と一致しました。コードに誤りはなさそうです。
20回の重みの更新の推移が次のグラフです。10回以前にすでに推定の収束が済んでいますね。なかなか優秀です。
# plot temp = result$log %>% gather(variable, value, 2:6) ggplot() + geom_line(aes(x = temp$k, y = temp$value, color = temp$variable))+ geom_line(aes(x = temp$k, y = temp$MSE * 150), color = "red", linetype = 2) + scale_y_continuous(sec.axis = sec_axis(~ . /150, name = "MSE")) + annotate("text", x = temp$k[1], y = temp$MSE[1] * 150 + 2, label = "MSE", color = "red")+ labs(y = "Estimate", x = "iteration", color = "variable")
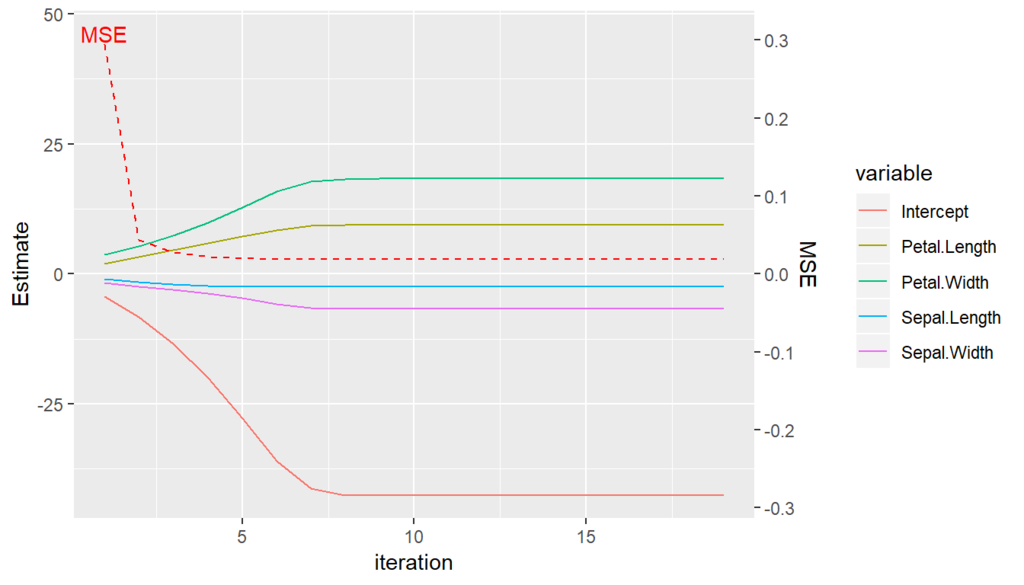
最終的なMSEは
str_c("MSE: ", result$MSE) # MSE
## [1] "MSE: 0.0188203802832454"
になりました。勾配降下法よりもいい感じです。
まとめ
- ロジスティック回帰は,対数尤度を負にした交差エントロピーを誤差関数に使う
- 交差エントロピーは(最小二乗法の平均二乗誤差とは違い)解析的に解を得られないので,勾配降下法かニュートン・ラフソン法でゴリゴリ計算していって数値的に解を出す
- Rの
glm()関数で採用されているのはニュートン法のほう。少ない反復回数でうまく収束してくれる。
参考
- ロジスティック回帰について
- IRLSについて
- IRLS法 - 機械学習の「朱鷺の杜Wiki」
- PRML 4.3.3節
- カステラ本 4.4.1節
対数法則:(1) \(\log (xy) = \log x + \log y\), (2) \(\log (x^p) = p \log x\)↩
\(\exp(-x)\)は\(e^{-x}\)と表記されることもあります。↩
この関数はロジスティック関数と呼ばれていたり,シグモイド関数と呼ばれていたり,ロジスティック・シグモイド関数(logistic sigmoid function)と呼ばれたりします。↩
\(\begin{align}\pi(\boldsymbol{x}) &= \exp(\boldsymbol{\beta}^{\top}\boldsymbol{x})(1-\pi(\boldsymbol{x})) \\&= \exp(\boldsymbol{\beta}^{\top}\boldsymbol{x})- \exp(\boldsymbol{\beta}^{\top}\boldsymbol{x}) \pi(\boldsymbol{x})\\ \pi(\boldsymbol{x}) + \exp(\boldsymbol{\beta}^{\top}\boldsymbol{x}) \pi(\boldsymbol{x})&= \exp(\boldsymbol{\beta}^{\top}\boldsymbol{x}) \\ \pi(\boldsymbol{x}) (1 + \exp(\boldsymbol{\beta}^{\top}\boldsymbol{x})) &=\exp(\boldsymbol{\beta}^{\top}\boldsymbol{x}) \\ \pi(\boldsymbol{x}) &=\frac{\exp(\boldsymbol{\beta}^{\top}\boldsymbol{x})}{1 + \exp(\boldsymbol{\beta}^{\top}\boldsymbol{x})} \end{align}\)↩
バッチ学習と呼ばれることもあります。ただし,名前が少し似ている確率的勾配降下法(stochastic gradient descent method: SGD,オンライン学習とも)はこれとは少し異なるアルゴリズムです。↩