データサイエンス（統計学・機械学習）を鳥瞰する

データサイエンス（ここでは統計学と機械学習をまとめてこう呼ぶことにします）をざっくりと眺めることを考えてみます。

1. 鳥瞰の仕方（分類の仕方）を考える
2. 鳥瞰する（分類して，ざっくり解説していく）

の流れになります。本題は2.のほうです。

1. まず分類する方法を考える

データサイエンスをどういう切り口で分類していくかを模索しています。

いまのところ，①ジャンルで整理していく方法，②その手法が果たす役割・目的で整理していく方法，の２つを考えています。

(1) ジャンルで整理

統計学なら「記述統計」「推測統計」「多変量解析」「時系列分析」…などという分け方，機械学習なら「ニューラルネット系」「決定木系」などという分け方（この分け方はイマイチな気がするが），あるいは「教師あり」「教師なし」などという分け方

といった具合に教科書などを参考にジャンル分けしていく方法があるかなと。

たとえば以下のような感じです。（厳密な分け方ではありませんが，だいたい合ってると思います）

このタイプのアプローチでは工藤（2013）がいい感じの表を作っていました。

また，統計検定の出題範囲表もこのような分類方法ですね。

(2) 機能・目的で整理

分析結果として何が得られるかで整理していくアプローチもあるかなと思います。

例えば「記述」「予測」「因果推論」…といった具合に。これなら統計学の手法でも機械学習の手法でも統一して分類していくことができます。

表にするなら，例えばこんなかんじでしょうか。だいぶスッキリまとまりました。

また，機能ごとに分けるのであればジャンルで整理するアプローチに比べて紹介していく項目数も減るため，同じ紙幅であったとしても図を載せる余裕が出やすく，視覚的に説明しやすいことも利点でしょう。

2. 目的別に分類する方法でざっくり解説

前節の後者のアプローチでざっくり述べていきます。

記述的分析（Descriptive Analytics）

記述的分析はデータから「何が起きたのか」を知るための分析です。この手法は，データの分布から現実世界の事象を想像することになるため，「データ」「正しい分析」「事象に関する知識（ドメイン知識）」が必要になります。

以下で具体的な分析手法の例とその解説を行っていきます。

記述統計

グラフを描いたり，平均値や相関係数などを算出したりしてデータの関係性を把握する方法です。

回帰分析

回帰分析は変数間の関係を知ることや，予測のために使われる手法です。

例えば図のように2変数（横軸をX，縦軸をYとします）があり，線形に規則性のある分布をしているデータがあるとき，

という関係を仮定して，この傾きの係数を推定する手法です。

それによって，例えば「が１増加したときに，は２増加している！」といった情報を得ることができます。

２変数だけでなく，もっと多くの変数の間の関係も同様に推定できるため，相関係数よりも強力な相関分析の手法です。

（回帰分析は(1)相関関係の分析，(2)因果関係の分析，(3)予測，のどれにも使える手法で，これは(1)の使い方をしています）

決定木

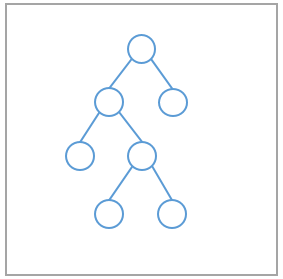
決定木は条件分岐によってデータの規則性を見つけていく方法です。

決定木は単体では「弱い学習器」と呼ばれる予測精度の低い分析手法ですが*1，条件分岐という人間の意思決定にも近いモデルでデータの関係を表現でき，記述的分析にも使われます。

分析の目的変数を表しているのが図の青い丸とオレンジの四角で，この例ではこの２つの値をとるものと想定しています。分析の説明変数は図のの変数で，これらが「いくつ以上のとき」といった条件でyes,noに分岐して目的変数を説明します。

例えば，目的変数が「サービスを退会した/しなかった」の２つの値だとしてみましょう。例えば，「年齢が50歳以上」で「年収が600万円以上」の領域（ユーザーのセグメント）では「サービスを退会する人が多くなる（退会する確率が高くなる）」といった情報を得ることができます。

教師なし学習

上の「回帰分析」や「決定木」は「教師あり学習」とも呼ばれるもので，「目的変数」が存在している状況での分析に使われます。

一方，「教師なし学習」は，目的変数が存在しない状況で，純粋にデータの分布から特徴を探索していく手法になります。

例えば主成分分析（principal component analysis：PCA）という手法があります。これはたくさんの変数があるデータから，それぞれの変数のもつ情報をまとめ，変数の数を減らす手法です。

変数の数を減らして何が嬉しいのかというと，例えば２変数にまで減らすことができれば，散布図などにすることができるためです。

例えば，自社の商品と他社の商品を比べたいとき，商品の特徴に関するデータをとってきたとしても，変数の数が多いと比較する基準が多すぎてよくわからなくなります。そこで，主成分分析などを使って変数の数を減らすことができれば，散布図を作ってポジショニングマップとして市場での立ち位置の異同を把握することができます。

診断的分析（Diagnostic Analytics）

データから，「なぜ起きたのか」を明らかにするのがこの分析の目的です。

データサイエンスでは，統計的因果推論という，データから物事の因果関係を推し量る方法があります。

医学など学術ではランダム化比較試験（RCT）というものが有名で，これはビジネスの世界ではA/Bテストという名前で呼ばれています。どういう手法かを以下で述べていきます。

まず，「因果関係がわかる理想的な状態とは何か」について考えてみましょう。例えば薬の効果を知りたいとき，ある時点のある人物（仮にAさんとします）を２人用意して，両者への処置を変えて「薬を与えられるAさん」，「薬を与えられないAさん」を用意して両者を比較すれば，Aさんにとっての薬の効果を知ることができそうです。

ただし，これは理想的な状態を考えているにすぎず，実際はある時点に同一人物を２人用意するのは不可能です（これを因果推論の根本問題といいます）。

この問題を回避するために，RCTでは，「薬を与えられるグループ」「薬を与えられないグループ」の２グループを用意し，被験者を両グループをへとランダムに割り振り，両グループでの効果を比較して薬の効果を推定します。

（同一時点に同一人物を２人用意することはできないが，ランダム割付を使えばグループの個体差を均等化して同一時点に同一グループと見なせるものを２つ用意することはできる，という考え）

予測的分析（Predictive Analytics）

「何が起こりそうか」など，予測を行う分析です。

教師あり学習

上で述べた回帰分析や決定木のように，予測の目的変数（回帰分析でいうと）がある場合の機械学習を教師あり学習と呼びます。

「次期に仕入れるべき商品の数量の予測」も，「画像に何が写っているかを予測（識別）」するのにもこのタイプの分析が使われています。

処方的分析（Prescriptive Analytics）

「何をすべきか」を明らかにするための分析です。予測的分析のあとの具体的な最適化を行います。

レコメンデーション

レコメンデーションシステムによる「おすすめ」の表示のことです。

レコメンデーションエンジンについては種類が豊富なので割愛します

異常検知

工場での不良品の検知や，インフラ整備現場において収集された画像データから亀裂箇所の発見など，異常な値を検知してアラートを出すための分析のことです。

その他予測的分析の結果の応用

他にも，「広告の閲覧者の情報（"20代，女性"など）を説明変数にしてクリック率の予測を行い，予測値が最も高い広告を配信する」，「顧客ごとの情報から成約率を予測し，予想成約率が高い顧客から優先的にセールスを投入する」などもあります。

参考

これからデータ分析を始めたい人のための本

*1:ちなみに，多数の決定木をまとめあげる派生手法が多数存在し，それらはきわめて強力な予測手法です