盆暗の学習記録

データサイエンス ，エンジニアリング，ビジネスについて日々学んだことの備忘録としていく予定です。初心者であり独学なので内容には誤りが含まれる可能性が大いにあります。

「統計的に有意」だけでは足りないワケ：バイアス－バリアンス分解のはなし

統計的因果推論 統計学 計量経済学 バイアス－バリアンス分解

機械学習の教科書には，序盤などに「バイアスとバリアンス」とか「バイアス－バリアンス分解」といった項目があります。「誤差にはバイアスとバリアンスの２種類があるよ」という話です。正直私はそれを読んでも「ふーん。まぁ，そうだよね」と思うくらいで特に重要なトピックとも思っていませんでした。

ところが，統計学にも「バイアスとバリアンス」の話があって，そちらは個人的に「なるほど！！」となったのでここにメモしておきます。

バイアス（bias）とバリアンス（variance）

MSEの展開

推定したい真のパラメータ \thetaとその推定量 \hat{\theta}の平均二乗誤差（Mean Squared Error：MSE） E[(\hat{\theta} - \theta)^2]を分解（展開）すると，以下のようになります。

 
\begin{align}
MSE(\hat{\theta}, \theta)
&= E[(\hat{\theta} - \theta)^2] \\
&= E[(\hat{\theta} - E[\hat{\theta}] + E[\hat{\theta}]-\theta)^2] \\
&= E[(\hat{\theta} - E[\hat{\theta}])^2] + [E[\hat{\theta}]-\theta]^2\\
&= Var(\hat{\theta}) + Bias(\hat{\theta},\theta)^2
\end{align}

ここで Var(\hat{\theta})はバリアンス（variance，普通に分散のこと）， Bias(\hat{\theta},\theta)はバイアス（bias）で，それぞれ

 
\begin{align}
Var(\hat{\theta}) &= E[(\hat{\theta} - E[\hat{\theta}])^2] \\
Bias(\hat{\theta},\theta) &= E[\hat{\theta}]-\theta
\end{align}

と定義されます。「パラメータの推定量と真の値との平均二乗誤差はバリアンスとバイアスの二乗の和である」ということです。

つまり？

「統計的に有意」かどうかの判断で使われる標準誤差（推定量の標準偏差） SE(\hat{\theta})は分散 Var(\hat{\theta})の平方根なので、ここに関わってきます。

上の分解は「パラメータの推定を誤る原因は，標準誤差とバイアスの2つに分けられる」ということであり，言い換えると，「『統計的に有意（分散が低い）』であっても推定が正しいとは限らない（バイアスが存在するかもしれない）」ということになります。これは非常に興味深いトピックです。

（ただし，標本平均のように不偏推定量（unbiased estimator）と呼ばれるタイプの推定量はバイアスがゼロなのでこの心配はありません。一方，回帰分析の最小二乗推定量などは不偏性を得るための前提が満たされにくいので問題になります。）

イメージ図

射的に例えてイメージ図を描くなら，以下のような感じでしょうか。的の中心が真の値 \thetaで，着弾点が推定量 \hat{\theta}です。

「バリアンスが低い（統計的に有意である）」ことが必ずしも「真の値をよく推定できている」と言えるとは限らないことがわかるかなと思います（右上の図）。

バリアンスを下げるには

「バリアンスを下げるにはどうしたらいいのか」を考えるために，まず，「標準誤差」ってなんだっけ，「統計的に有意」ってなんだっけ，というところの用語の確認から行っていきます。回帰分析での推定を例に考えていきます。

標準誤差

標準誤差（standard error）はパラメータの推定量と真の値とのばらつき（標準偏差）のことです。

回帰分析の場合，誤差項 \varepsilon_iの分布について

 
\varepsilon\_i \sim N(0, \sigma^2)

という仮定をおくと，傾き係数 \hat{\beta_1}の分布は

 
\hat{\beta\_1} \sim ~ N\left(\beta\_1, \frac{\sigma^2}{\sum^n\_{i=1}(X\_i-\bar{X})^2}\right)

となることが知られています。

誤差項 \varepsilon_iの分散 \sigma^2の不偏推定量 \hat{\sigma}^2は，回帰分析の残差 \hat{u}_i = Y_i - (\hat{\beta}_0+\hat{\beta}_1X_i)から得られることが知られていて，以下のようになります。

 
\hat{\sigma}^2 = \frac{\sum\_{i=1}^n\hat{u}\_i}{n-2}

これを用いると，推定量 \hat{\beta}_1の標準誤差は

 
SE(\hat{\beta}\_1) = \sqrt{\frac{\hat{\sigma}^2}{\sum^n\_{i=1}(X\_i-\bar{X})^2}}

となります。

「統計的に有意」かどうかは， t検定の場合，推定量（と帰無仮説で想定する真の値の差）を標準誤差で割って得る t値（推定量のばらつきに対する推定量の大きさ）から判断します。

バリアンスを下げるには

バリアンスを下げるには，どうすればよいのでしょうか。

標準誤差 SE(\hat{\beta}_1)は，言い換えれば

 
SE(\hat{\beta}\_1) = \sqrt{\frac{\hat{\sigma}^2}{\sum^n\_{i=1}(X\_i-\bar{X})^2}} = \sqrt{\frac{\text{誤差項のばらつき}}{\text{データのばらつき}}}

で，「誤差項のばらつき」 \hat{\sigma}^2は

 
\hat{\sigma}^2 = \frac{\sum\_{i=1}^n\hat{u}\_i}{n-2} = \frac{\text{予測精度の低さ}}{\text{サンプルサイズの大きさ}}

になります。つまり，バリアンスを下げるには，

  • サンプルサイズを上げて \hat{\sigma}^2を下げる
  • 予測精度を上げて残差 \hat{u}_iを下げる

という方法が考えられます。

例えば手元にモデルに入れていない変数がある場合に投入してみて残差を減らしてみたり，とかです。

バイアスを下げるには

「バイアスを回避するにはどうしたらよいのか」，あるいは「そもそもどういうときにバイアスが発生するのか」といったことについて考えてみます。

バイアスの種類と原因

１．欠落変数バイアス（除外変数バイアス）

本来なら説明変数としてモデルに含まれるべき変数が欠落しているために誤差項と説明変数が独立でなくなり生じるバイアスを欠落変数バイアス（omitted variable bias）と呼びます。

例えば X\to Yへの因果関係を見たいとき， X,Yの両方に影響を与える変数があるとき，これを交絡変数（confounding variable）と呼びます（交絡因子とも呼ばれます）。交絡変数があるときは，モデルに含めないと欠落変数バイアスが生じます。

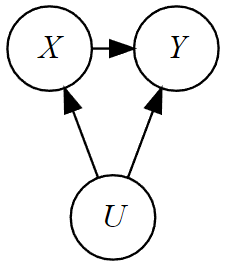
f:id:nigimitama:20210227162055p:plain

２．同時決定バイアス

被説明変数と説明変数が相互に影響を与え合っている（因果関係がループしている）関係にあるときもまた誤差項と説明変数が独立でなくなり，バイアスを生みます。

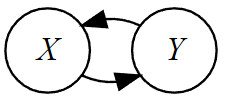
f:id:nigimitama:20210227162000p:plain

３．内生性バイアス（逆の因果性）

説明変数に使用している変数が内生変数（想定しているモデルの中で内生的に決定される変数で，被説明変数に該当する）である場合も誤差項と説明変数が独立でなくなり，バイアスを生じます。

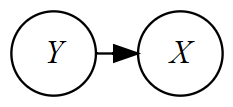
f:id:nigimitama:20210227162042p:plain

バックドア基準

バイアスを避けるには，データが生成されている構造をしっかりと捉えて，上記のバイアスを生むことがないように統計モデルを構築する必要があります。その際に参考になる変数選択基準がバックドア基準というものです。

バックドア基準

原因をX，結果をYと表すとき， 1. 追加した説明変数はXの子孫（下流側）ではない 2. （Xから出る矢印を除いたときの因果構造において） 追加した説明変数によってXとYの交絡因子からの流れをすべて遮断できている

バックドア基準については林岳彦先生のスライドや岩波データサイエンスVol.3での記事がわかりやすいのでおすすめです（岩波の記事はこのスライドと中身ほぼ一緒です）。

『バックドア基準の入門』＠統数研研究集会 - SlideShare

今回の話から導かれる推定の３つの方向性

（※この先の記述は他に明示している文書を見たことがないので私の推測です）

「『統計的に有意』であればその推定が正しいわけではない」という点から生まれる「ではどう推定していくべきか」についての考え方は，私が知る範囲では３つあります。

１．実験（ランダム化比較試験・A/Bテスト）

実験（ランダム化比較試験：効果を測定したい処置を行うグループへの被験者の割付をランダムに行う）によってデータの生成構造をコントロールし，バイアスを回避するアプローチです。

２．準実験・擬似実験

計量経済学では「実験（ランダム化比較試験）を行いたいが，分野の都合上，実験は難しい」という分野の特性に合わせて，観測データから「実験に似た状況（ランダム割付が発生している状況）を探し出し，実験したとみなす」ような手法をとることもあります。

実験と見なせる状況は観測されたデータのうちごく一部になってしまうので，局所的（一部の主体への）平均因果効果の推定になってしまうことも多いですが，「ランダム化されているのでバイアスは除去できている」という点は分析上強い武器になります。

３．統計モデリング

現実のデータ生成構造をうまく模すことができない統計モデルを組んで推定を行うと，パラメータにバイアスが含まれます。なので，データを良く見て正しい統計モデリングを行おうという話です。

計量経済学では実験的なアプローチが導入される前のパラダイムではこの方向性が主流でした。しかし，例えばバイアスを生む原因となる要因が観測不可能なものである場合に対処がきわめて難しくなるなど，限界はあります（例えばその人の「知性」や「健康への関心の高さ」という明示的にデータにできないものが交絡因子であると考えられるときにどう統計モデルに組み込むか）。

まとめ

  • パラメータの真の値と推定量の誤差（MSE）は，バイアスとバリアンスに分けられる
  • 「バリアンスが小さい（統計的に有意）」かつ「バイアスがない」推定量が良い推定量
  • バイアスの回避のためには，いろいろアプローチがあり，できれば実験が望ましい

参考