2025-09-14

LintやFormat、型チェックを自動実行する方法まとめ

エンジニアリング Python

lintや型チェックなどの静的解析はバグを未然に防ぐのに役立ちますし、formatterの実行は規約に反するコードを自動で修正してきれいなコードベースを保つうえで便利です。

しかし、コードを変更するたびに手動でコマンドを実行するのは面倒なので、自動で実行したいです。

LintやFormatを自動化する方法をいくつかまとめます（主にPython向けですが、他の言語でも考え方は同じです）

VS Codeで実行する
- 拡張機能の導入
- Formatter の実行
commit 時に Git hook で実行する
Github Actions で実行する
- 静的解析をGithub Actionsで実行する
- pre-commitをGithub Actionsで実行する

VS Codeで実行する

拡張機能の導入

VS Code を使っている場合、拡張機能で Lint や Format、型チェックの機能を簡単に導入できます。

例えば

Python の Lint & Format → Ruff
Javasctipt、Markdown、YAML などの Lint & Format → Prettier
Python の型チェック → Pylance

などを導入するとファイルの編集中に自動的に静的解析が実行され、Lint や型チェックが機能します。

なお Pylance はデフォルトで型チェックが off になっているため VS Code の Settingsにおける python.analysis.typeCheckingMode の項目で base 以上の設定に変更する必要があります。

Formatter の実行

手動実行する場合は右クリックのメニューから「Format Document」をクリックします。

自動実行させたい場合、VS Code の Settings に行き、editor.formatOnSave という項目にチェックを入れます。こうするとファイルの保存時に Formatter が実行されるようになります。

workspace の setting として設定した場合、.vscode/settings.json が作成されて保存されます。逆にこのjsonを書き換えることでSettingsに反映させたりできます。

// .vscode/settings.json
{
    // 型チェック
    "python.analysis.typeCheckingMode": "standard",
    // Linting
    "editor.formatOnSave": true,
    "ruff.lineLength": 120
}

commit 時に Git hook で実行する

Git hook は gitのcommitやpushなどを実行する前後に別の処理を実行させる設定のことです。

commitの前に指定した処理（LintやFormat）を実行させたい場合、pre-commit フレームワークを使うことで簡単にgit hookを設定できます。

1. pre-commitのインストール

pre-commitはPyPIで公開されており、pipやuvでインストールできます

# pipの場合の例
pip install pre-commit
# uvの場合の例
uv add pre-commit --dev

2. 設定ファイルの作成

.pre-commit-config.yaml を作成し、そこに実行したい処理の設定を入れます。github リポジトリを紐づける形になります。

例えば ruff でLintとFormatを、 pyright で型チェックをする場合は次のようにします。

repos:
- repo: https://github.com/astral-sh/ruff-pre-commit
  rev: v0.13.0
  hooks:
  - id: ruff-format
  - id: ruff-check
    args: [--fix, --exit-non-zero-on-fix]

- repo: https://github.com/northisup/pyright-pretty
  rev: v0.1.0
  hooks:
  - id: pyright-pretty

これでcommitの実行時にチェックが走るようになります。パスしなければcommitできなくなるので、ある程度厳密に静的解析を運用したいときに向きます。

$ git commit
ruff format..............................................................Passed
ruff check...............................................................Passed
Python type checker [pyright]............................................Passed

Github Actions で実行する

静的解析をGithub Actionsで実行する

静的解析のパッケージをGithub Actions環境にインストールして実行することでpush時に実行できます

name: Lint & Typecheck (Python)

on:
  pull_request:
  push:
    branches: [main]

jobs:
  lint:
    runs-on: ubuntu-latest
    steps:
      - uses: actions/checkout@v4
      - uses: actions/setup-python@v5
        with:
          python-version: "3.12"
          cache: "pip"
      - run: pip install -U pip
      - run: pip install ruff pyright
      - run: ruff check
      - run: pyright .

pre-commitをGithub Actionsで実行する

また、pre-commitをGithub Actionsで実行するという方法もあります。

パッケージをpipで管理している場合は pre-commit/action を使うと楽かもしれません。

uvを使っている場合は astral-sh/setup-uv のあとに uv run pre-commit run を実行すればよいです。

name: pre-commit

on:
  pull_request:
  push:
    branches: [main]

jobs:
  pre-commit:
    runs-on: ubuntu-latest
    steps:
    - uses: actions/checkout@v4
    - uses: astral-sh/setup-uv@v6
    # devDependencies環境のもとでpre-commitを実行
    - run: uv run --group dev pre-commit run --show-diff-on-failure --all-files

GitHub CI/CD実践ガイド――持続可能なソフトウェア開発を支えるGitHub Actionsの設計と運用エンジニア選書

作者:野村友規
技術評論社

Amazon

2025-09-02

Overleafをローカル環境で起動する

環境構築

OverleafはWebブラウザ上でLaTeXの文書を作成・共同編集できるとても便利なLaTeXエディタです。

OverleafはWebサービスとして提供されていますが、オープンソースのエディタであるため自分のPC上で立ち上げることもできます。

ローカルで起動する場合は共同編集はできませんが、自分ひとりで簡易的に使いたい場合は十分な機能を持っています。

環境構築手順
使ってみる
日本語対応する
- 一時的な対応
- 恒久的な対応
  - 方法1. 自分でDockerfileを書く（おすすめ）
  - 方法2. DockerHub上の日本語対応イメージを指定する
参考

環境構築手順

0. 前提

環境構築には次のものが必要です

git
docker

1. リポジトリをcloneします

overleaf/toolkit をcloneします。

git clone https://github.com/overleaf/toolkit.git ./overleaf-toolkit

cd ./overleaf-toolkit

2. bin/initを実行し、configファイルを作ります

bin/init

3. bin/up を実行するとdocker composeが動いてOverleafが起動します

bin/up

http://localhost からアクセスできるようになります。

使ってみる

アクセスしたらまずログインフォームが出てくるので、まずアカウントを作る必要があります。

初回は http://localhost/launchpad でAdminユーザーの作成を行います。

ローカルに保存されるだけの情報なのでテキトーに hoge@example.com と password とかで大丈夫だと思います。

あとはログインして普通のOverleafと同様にProjectを作って使えばOKです。

日本語対応する

Webサービスとして提供されているOverleafとはバックエンドで動いているLaTeXの環境が若干異なるようです。

とくに日本語はそのままだと全く使えないのでフォントなどを入れてあげる必要があります。

一時的な対応

手っ取り早い対応としては、起動中のoverleafのDockerコンテナに入って日本語文書用のファイルをダウンロードする方法です。

# Dockerコンテナに入る
bin/shell
# docker exec -it sharelatex bash でも可

# パッケージマネージャを更新
tlmgr update --self

# LuaLaTeX系の日本語パッケージ等をインストール
tlmgr install \
  collection-luatex \
  collection-langjapanese \
  xkeyval

Recompileすると、すぐ反映されてエラーなく日本語の文書が作れるようになっています。

なお上記はコンパイラをLuaLaTeXにしていることを前提としているので、Overleafの左上の「Menu」ボタンから設定を開いてコンパイラをLuaLaTeXに変更する必要があります。

恒久的な対応

方法1. 自分でDockerfileを書く（おすすめ）

./config/ に docker-compose.override.yml というファイルを作って変更したい要素を書けばコンテナ環境を変更できます。

まず、 ./config/ にDockerfileと docker-compose.override.ymlを作成します。

./config
├── Dockerfile
├── docker-compose.override.yml
...

./config/Dockerfile は公式のイメージに日本語パッケージを追加するように書いておきます

FROM sharelatex/sharelatex:latest

# コンテナのパッケージマネージャを更新
RUN tlmgr update --self

# LuaLaTeX系の日本語パッケージ等をインストール
RUN tlmgr install \
    collection-luatex \
    collection-langjapanese \
    xkeyval

./config/docker-compose.override.yml には作成したDockerfileを使ってビルドするように書いておきます。

services:
  sharelatex:
    build:
      context: ..
      dockerfile: config/Dockerfile
    # ビルドしたイメージに名前をつける（必須）
    image: local/my-sharelatex:latest

image:の部分に書くイメージ名は適当で大丈夫そうですが、省略してしまうと bin/up したときにoverrideがうまく働かなかったので項目自体は必須のようです。

これで立ち上げると日本語対応できているはずです。

方法2. DockerHub上の日本語対応イメージを指定する

もっと楽な、自分でDockerfileを書かなくていい方法としては、日本語対応済みのOverleafのDockerImageをDockerHubから拾ってくる方法です。

config/overleaf.rc の OVERLEAF_IMAGE_NAMEという変数を書き換えることで参照先を変更できます。（デフォルトは公式のsharelatex/sharelatex です）

例えば tuetenk0pp/sharelatex-full は公式イメージ sharelatex/sharelatex に TeX Liveのfullを足し合わせたイメージとなっているので、これを参照すれば日本語対応できます（なおTeX Liveのfullはファイルサイズが大きく、上記Imageは約14GBあるのでご注意を）。

# Uncomment the OVERLEAF_IMAGE_NAME variable to use a user-defined image.
OVERLEAF_IMAGE_NAME=tuetenk0pp/sharelatex-full

⚠️ただし、こうした非公式Docker Imageは性善説が前提となる（セキュリティリスクがある）のと、数年後には更新されなくなっていて代替を探す必要が出てきたりすることもよくありますので注意が必要です。

参考

https://ja.overleaf.com/learn/latex/Japanese

［改訂第9版］LaTeX美文書作成入門

作者:奥村晴彦,黒木裕介
技術評論社

Amazon

2025-08-10

相関の希薄化とバイシリアル相関係数

統計学

相関の希薄化という現象と、それに対処する方法の一つである「バイシリアル相関係数」の構造についてメモ

相関の希薄化
カテゴリカル変数の相関の希薄化
二値化による相関の希薄化
バイシリアル相関係数
二値ではなく多値の場合は…？
参考文献

相関の希薄化

相関の希薄化（attenuation of correlation） とは、データの測定誤差によって2つの確率変数 $X$ , $Y$ の間の積率相関係数がゼロに近づく方向のバイアスをもつ現象です。

Spearman (1904) によって提案された希薄化を修正する式は次のようになっています。

$\rho_{xy} = \frac{r_{xy}}{\sqrt{r_{xx}} \sqrt{r_{yy}}}$

$r_{xy}$ ：観測された相関
$\rho_{xy}$ ：真の相関、あるいは信頼性が完璧なもとでの相関
$r_{xx}$ ：変数 $X$ の信頼性（測定誤差の少なさ）
$r_{yy}$ ：変数 $Y$ の信頼性（測定誤差の少なさ）

この式を変形すると

$r_{xy} = \rho_{xy} \sqrt{r_{xx}} \sqrt{r_{yy}}$

となり、観測される相関係数は真の相関係数に対して、測定の信頼性の影響を受けている構造であることがわかります。

この信頼性をどう得るのかについては、例えば古典的テスト理論においては再テスト法（例えば $x$ を再び測定したときの相関 = $r_{xx}$ ）や信頼性係数といった方法についての議論が広がっていったようです。しかし本記事ではカテゴリカル変数の相関係数に焦点を当てたいと思います。

カテゴリカル変数の相関の希薄化

相関を測りたい確率変数にカテゴリカル変数（質的変数）が含まれており、かつそれが「もともと連続変数だったものが離散化された形で観測された」と考えられるものだった場合、本来よりも解像度が粗い測定をしているので信頼性が低い（測定誤差が大きい）ということで相関の希薄化の問題が生じます。

「もともと連続変数だったものが離散化された形で観測された」というのは、例えば次のようなデータです：

例1（満足度のアンケート）：回答者の心の中にある「満足度」が質問紙の「満足」「やや満足」「どちらでもない」などの離散的な選択肢によって離散化された形で観測されている
例2（英語の試験の設問）：ざっくり言えば、回答者の「英語力」が高いなら設問への回答が「正解」を選ぶ傾向が高くなり逆も然りとなる → 正解・不正解の二値へ離散化された形で英語力が観測されていると考えられる

二値化による相関の希薄化

連続変数を離散化したときにどのくらい相関が希薄化されるかは、もともとの連続変数が従う分布や離散化の閾値の取り方などによって異なります。

例えば相関係数 $\rho$ の2変量正規分布に従う連続変数 $X$ , $Y$ のうち片方の変数、例えば $Y$ を標準化して、分布の中央の点（平均値 = 中央値）を閾値に2等分するように二値化して $Y_d$ とおくことにします。この場合、観測される積率相関係数 $r = \operatorname{Cov}(X, Y_d)$ と元々の相関係数 $\rho$ は

$r = 0.798 \rho$

という関係にあることが報告されています（Peters & Van Voorhis, 1940）。

実際に2変量正規分布からの疑似乱数を生成させて二値化して実験してみてもそのような結果になります。

import numpy as np
from scipy.stats import pearsonr

# 正規分布からのサンプリング
rho = 0.5 # 真の相関係数
np.random.seed(0)
data = np.random.multivariate_normal(mean=[1, 5], cov=[[1, rho], [rho, 1]], size=100_000)
x, y = data[:, 0], data[:, 1]

# 平均値を閾値に二値化
yd = 1 * (y >= y.mean())
r = pearsonr(x, yd)[0]  # 二値化後の相関係数
print(f"真の相関={rho:.3f}, 二値化後の相関係数={r:.3f}, 比率={r/rho:.3f}")

真の相関=0.500, 二値化後の相関係数=0.399, 比率=0.798

真の相関係数の条件を変えて（ $-0.5, 0.25, 0.75$ の3条件で）、また疑似乱数の生成回数を増やしてモンテカルロシミュレーションしてみます（1回のサンプル数=10,000、試行回数=10,000）。

いずれの場合も、二値化後のピアソンの積率相関係数 $r$ は真の相関 $\rho$ よりゼロに近い値へと希薄化されており、二値化後の相関係数と真の相関の比率は0.798となっています。

この0.798という値は閾値の位置によって異なりますが、一般化すると

$e(p) = \frac{\phi(z)}{\sqrt{p(1 - p)}}$

$p$ ：二値化後の変数で閾値より上の値の比率。例えば $Y_d \in \lbrace 0,1 \rbrace$ なら $p = E[Y_d$ ]
$\phi(z)$ ：標準正規分布の確率密度関数。 $z$ は閾値の正規分布上の位置（例：平均値が閾値なら $z = 0$ ）

という関数であることが知られています（Cohen, 1983）。

バイシリアル 相関係数

相関の希薄化の問題に対処している相関係数のひとつに バイシリアル（biserial）相関係数 というものがあります。これは前節の「正規分布に従う連続変数を二値化したカテゴリカル変数と連続値の間の相関」を測る相関係数で、

$r_{\text{bi}} := r_{\text{Pearson}} \times \frac{\sqrt{p(1 - p)}}{\phi(z)}$

という相関係数になります。

これはちょうどピアソンの積率相関係数 $r_{\text{Pearson}}$ を前述の希薄化の影響 $e(p)$ の逆数で補正をかけた構造になっています。

私がバイシリアル相関係数の式を初めて見たときはなぜこういう式にしているのかがさっぱりわかりませんでしたが、相関の希薄化のことを知っていれば「既知の量のバイアスが入るから補正しよう」というかなり素直な式をしていることがわかります。

二値ではなく多値の場合は…？

二値化ではなく、任意のカテゴリ数への離散化の場合はどうすればいいのでしょうか。その場合に向けて一般化した相関係数も存在します。

連続変数とカテゴリカル変数の相関 → ポリシリアル（polyserial）相関係数
カテゴリカル変数とカテゴリカル変数の相関 → ポリコリック（polychoric）相関係数

なお、これらの相関係数は明示的に補正係数を掛けるバイシリアル相関係数とは異なり、「正規分布に従う変数が任意の閾値で区切られて観測された」という状況をモデリングし、そのモデルのもとで最も当てはまりがいい相関係数を最尤推定するアプローチをとっています（詳しくは Drasgow 1986 などをご参照ください）。

また、バイシリアル、ポリシリアル、ポリコリックなどの相関係数をPythonで実行できるライブラリを作ったことがあるのでもしご興味のある方はご利用ください。

github.com

参考文献

Cohen, J. (1983). The cost of dichotomization. Applied psychological measurement, 7(3), 249-253.
Drasgow, F. (1986). Polychoric and polyserial correlations In: Kotz S, Johnson N, editors. The Encyclopedia of Statistics.
Spearman, C. (1904). The proof and measurement of association between two things. Am J Psychol, 15, 72-101.
Peters, C. C., & Van Voorhis, W. R. (1940). Statistical procedures and their mathematical bases. McGraw-Hill.

2025-08-07

FastAPIを使ってOpenAPI仕様書と、TypeScriptクライアントを自動生成する

エンジニアリング

FastAPIを使うと色々便利そうだなとあらためて認識して触ってたのでメモしておきます。

FastAPI → OpenAPI仕様書
OpenAPI → TypeScriptのクライアント
- OpenAPI TypeScript
- @hey-api/openapi-ts
OpenAPI → テスト（余談）

FastAPI → OpenAPI仕様書

FastAPIはPythonでのWebAPI開発が簡単にできるフレームワークです。

Pythonの型ヒントをもとにデータ型のバリデーションもしてくれて、簡潔なコードでAPI開発ができます。

from fastapi import FastAPI
from typing import Literal

app = FastAPI()

Animal = Literal["cat", "dog", "bird"]

@app.get("/favorite-animal")
async def favorite(name: Animal) -> str:
    return f"{name}s are cute!"

FastAPIの便利機能の一つが、ソースコードからOpenAPIによる仕様書を自動生成してくれる点です。

fastapi.tiangolo.com

これにより仕様書を自分で書く必要がなくなります。

OpenAPI → TypeScriptのクライアント

フロントエンド側でAPIを呼び出すコードをTypeScriptで書く場合もOpenAPIがあると役立ちます。

OpenAPI TypeScript

OpenAPI TypeScript を使うと、APIのメソッドの入出力の型定義ファイルを生成できます。

インストール

npm i -D openapi-typescript typescript

tsconfig.json も追加します。

{
  "compilerOptions": {
    "module": "ESNext",
    "moduleResolution": "Bundler",
    "noUncheckedIndexedAccess": true
  }
}

型定義ファイルの生成

次のコマンドで型定義ファイルを生成できます。生成されるのは.d.tsファイル1つだけです。

npx openapi-typescript ./path/to/my/openapi.json -o ./path/to/my/schema.d.ts

openapi-fetch

OpenAPI TypeScriptはfetchやSWRやTanStack Quaryのラッパーの生成機能もあります。

npm i openapi-fetch

import createClient from "openapi-fetch";
import type { paths } from "./my-schema"; // 生成したd.tsファイル
const client = createClient<paths>({ baseUrl: "https://myapi.dev/v1/" });
const { data,  error } = await client.GET("/blogposts/{post_id}", {
  params: { path: { post_id: "123" }  },
});

非常に便利です。

openapi-ts.dev

@hey-api/openapi-ts

@hey-api/openapi-ts はOpenAPI TypeScriptよりも明示的にクライアントコードを生成するパッケージです。

https://github.com/hey-api/openapi-ts

まだ発展途上のようですが、頻繁にアップデートされています。

次のコマンドでデモを実行することができます。

npx @hey-api/openapi-ts \
  -i https://get.heyapi.dev/hey-api/backend \
  -o src/client

こんな感じでたくさんコードが生成されます。

src
└── client
    ├── client
    │   ├── client.ts
    │   ├── index.ts
    │   ├── types.ts
    │   └── utils.ts
    ├── client.gen.ts
    ├── core
    │   ├── auth.ts
    │   ├── bodySerializer.ts
    │   ├── params.ts
    │   ├── pathSerializer.ts
    │   └── types.ts
    ├── index.ts
    ├── sdk.gen.ts
    └── types.gen.ts

ただ、少し使ってみたところ、シンプルなAPIに対してでも多量のコードが生成され、認証がないAPIについても認証についてのコードが生成されるなど、個人的にはよくわからない挙動があったりで使いにくく感じました（理解が深まれば問題ないのかもしれませんが、学習コストが高そう）

OpenAPI → テスト（余談）

ちなみに、OpenAPIから property-based testing（PBT；仕様書通りの入出力ができるかのテスト）ができる Schemathesis というパッケージも存在します。

schemathesis.readthedocs.io

導入がとても簡単で、コマンドから実行したり

schemathesis run https://your-api.com/openapi.json

pytestで実行するスクリプトを作ったり

import schemathesis
schema = schemathesis.openapi.from_url("https://your-api.com/openapi.json")

@schema.parametrize()
def test_api(case):
    case.call_and_validate()  # Finds bugs automatically

Github Actionsに3行足すだけで実行できたりします

- uses: schemathesis/action@v2
  with:
    schema: "https://your-api.com/openapi.json"

ただ、FastAPIから作成したOpenAPI仕様書だと両者の間に差異は無いはずなので、多くの場合でPBTはパスします。そのため有効性はあんまり高くない気がします…。

私が簡単に試した感じでは、Pythonにおいてはboolがintのsubclassであるのに対してSchemathesisのテストではboolとintを明確に区別することを期待していた関係でそこだけFailしてました。

2025-07-12

カテゴリカル因子分析の概要とPythonでの実践方法

統計学 Python

今年に入ってから順序尺度の離散変数×連続変数の相関係数についてのライブラリを作ったり記事を書いたりしています。

nigimitama.hatenablog.jp

「こんなマニアックな相関係数をどこで使うんだ？」 と感じる方が多いかも…と思ったので、主要な応用例であるカテゴリカル因子分析について書いてみます。

因子分析

まず因子分析について簡単に説明します。因子分析は観測した変数 $x$ を切片パラメータ $\tau$ 、因子負荷量とよばれるパラメータ $\lambda$ 、共通因子スコア $f$ 、独自因子スコア $\varepsilon$ （誤差項のようなもの）の線形和によるモデルで

$\displaystyle x = \tau + \lambda f + \varepsilon$

のように表すモデルです。切片と傾きがある線形モデルなので回帰分析と形は似ていますが、 回帰分析の説明変数に相当する部分 $f$ が潜在変数（パラメータとしてモデルで推定する値） になっています。

この（共通）因子スコア $f$ が各観測値（例えばアンケートの各回答者）ごとに求まるので、観測対象のスコアリングに使用されます。例えば回答者の性格特性を評価したり（5因子性格モデル)）、「消費者が企業のどういった要因（因子）を魅力的に感じているか」の分析（例：北見ほか（2017）「企業の魅力要素と購買行動の考察」、日本マーケティング学会）に使われたりします。

なお、通常は $x$ は平均0、分散1に標準化した値 $z$ に変換して使うので切片は含めず

$\displaystyle z = \lambda f + \varepsilon$

のように書きます。上記は 1因子モデル と呼ばれるもので、複数の因子があるモデルも存在します。

観測変数の次元と因子の数を複数に一般化して行列で表記すると

$\displaystyle \mathbf{z} = \mathbf{\Lambda} \mathbf{f} + \boldsymbol{\varepsilon}$

となります。

因子分析では、観測変数の分散共分散行列（標準化している場合は相関係数行列） $\mathbf{\Sigma}$ をこのモデルで

$\displaystyle \mathbf{\Sigma} = \mathbf{\Lambda \Lambda^\top} + \mathbf{\Psi}$

のように構造化し、最尤推定法などでパラメータたち（ $\mathbf{\Lambda},\mathbf{\Psi}, \mathbf{f}$ ）を推定していきます（ここで $\mathbf{\Psi} = \operatorname{Var}[\boldsymbol{\varepsilon}$ ] ）。

カテゴリカル因子分析とは？

さて、本題のカテゴリカル因子分析は、アンケートデータで出てくる

「1（全くそう思わない）」〜「5（非常にそう思う）」のリッカート尺度
「ある／ない」「はい／いいえ」の2値データ
評価カテゴリ（例：低・中・高）

などの （順序尺度の）カテゴリカルな観測変数 をもとにして因子スコアを推定する手法です。

前述のように、因子分析では相関係数行列をパラメータで線形モデルへと構造化してパラメータを推定していきます。そのため、 相関係数さえ求まればあとは通常の因子分析と同じ方法が適用可能 です。

ここで「カテゴリカル変数同士の相関係数（ポリコリック相関係数）」、あるいは「カテゴリカル変数と連続変数の相関係数（ポリシリアル相関係数）」が使えるわけです。

ポリコリック相関係数もポリシリアル相関係数も、カテゴリカルな観測変数の背後には潜在的な連続変数が存在していて、ある閾値を超えるかどうかで離散的な観測変数の値が選ばれると仮定します。因子分析では潜在的な連続変数である因子スコア $\mathbf{f}$ を推定するのが目的であるため、この仮定とも整合的なユースケースになります。

実装例

データの例として、Rのpsychパッケージのサンプルデータセット bfi を使います。これは 5因子性格モデル（OCEAN） に基づいたアンケートデータで、25個の性格項目（各5問 × 5因子）を含みます。

A1 ～ A5：Agreeableness（協調性）
C1 ～ C5：Conscientiousness（誠実性）
E1 ～ E5：Extraversion（外向性）
N1 ～ N5：Neuroticism（神経症傾向）
O1 ～ O5：Openness（開放性）

RのデータセットはPythonのstatsmodelsパッケージから簡単に取得できます。

import statsmodels.api as sm

# psychパッケージの Big Five Inventory（性格5因子） データ
df = sm.datasets.get_rdataset("bfi", package="psych").data
df

次元数がやや多くて結果が見づらくなるので、簡単化のために2因子（10変数）までにしておきます

df = df.iloc[:, 0:10].dropna()

このデータは5段階のリッカート尺度（「非常にそう思う」や「全くそう思わない」といった選択肢を選ぶ）のため、値が5段階のカテゴリになっています。 5段階程度あればピアソンの積率相関係数を使って通常の因子分析をしてもカテゴリカルな相関行列を使ったときとの差があまりないことが知られていて（萩生田 & 繁桝 (1996)）、カテゴリカル因子分析が真価を発揮するのは4段階以下のデータのときではあるのですが、今回はこのデータでやってみます。

ordinalcorr パッケージを使って相関係数行列を求めます。

from ordinalcorr import hetcor
corr = hetcor(df)
corr.style.format("{:.3f}").background_gradient()

算出した相関係数行列を使って因子分析（→カテゴリカル因子分析）します

from statsmodels.multivariate.factor import Factor
fa = Factor(corr=corr, n_factor=2, method="ml").fit()
fa.rotate("varimax")

get_loadings_frame()で因子負荷量（factor loadings）を見ることができます。1~5番目までの変数（設問）が第1因子（協調性）に、6~10番目が第2因子（誠実性）に強く関係している様子がわかります。

fa.get_loadings_frame().format("{:.3f}").set_caption("因子負荷量")

factor_scoring()を使うと因子スコアも得られます。

import pandas as pd

factors_ = fa.factor_scoring(df, transform=False)
pd.DataFrame(factors_).head().style.format("{:.3f}").set_caption("因子スコア")

まとめ

以上のように、カテゴリカル因子分析では

相関係数行列を推定する
因子分析にかける

という手順で分析されるため、1.の相関係数行列を求めるときに ordinalcorrパッケージが役立つ、というわけです。

カテゴリカルデータを扱う機会がありましたらぜひ使ってみてください

github.com

2025-05-04

モンハンワイルズに学ぶUI設計

UI/UXデザイン

皆さんはモンハンしてますでしょうか。私はかなりハマっております。歴戦王のチャレンジクエストの実装が楽しみですね。

モンハンワイルズ、ゲームとしては楽しいのですが、UIがイマイチというか、とてもストレスフルに感じております。

私自身もWebアプリを開発していくなかでクソUIを量産していると思うのですが、モンハンで遊ぶことはユーザー側の気持ちを体感するよい機会になっています。

本記事ではモンハンワイルズのUIのどこがストレスに感じるのかをユーザー目線で言語化し、反面教師として開発者目線で 「自分がUIを作るときはここを気をつけよう」 というポイントを考えてまとめていきたいと思います。

操作に一貫性をもたせる
- ❌イマイチなところ：操作に一貫性がない
- ⭕️気をつけたい点：操作の一貫性と予測可能性
原則、オブジェクト指向のUIにする
- ❌️イマイチなところ：タスク指向のUI
- ⭕️気をつけたい点：まずオブジェクト指向のUIを検討する
繰り返し発生する操作には「一括操作ボタン」をつける
まとめ

（※なお筆者は「キーボード+マウス」でプレイしております。もしかしたらPS5ならあまり違和感ないかもしれません）

操作に一貫性をもたせる

❌イマイチなところ：操作に一貫性がない

例1：通常、マップはMキーで開くのですが、「マップ上にモンスターが出現した」「モンスターが立ち去りそう」などの マップと関連する内容の通知が出ているときは「マップを開くボタン（Mキー）」を押してもマップが開きません 。通知のToastが出ている間（通知の個数×数秒間の間）は マップを開くためには「通知を開くボタン（Yキー）」を押す必要があります 。

例2：メニューから選択肢を選ぶとき、多くの画面では移動するボタン（WASDキー）で選択肢を選ぶことができます（キャンプ内など）。

しかし、 NPCに話しかけて開くタイプのメニューでは移動するときのボタンは使えなくなります（WASDではなくマウスで選ぶことになります）

慣れの問題でもあるのですが、150時間プレイした現時点でも未だに慣れないUIです。

⭕️気をつけたい点：操作の一貫性と予測可能性

この点から学べることは「一貫性と予測可能性をもたせたUIにすること」です。

✅ユーザーがある画面で使えた操作方法は、他の類似画面でも使えるようにする
✅普段使えている機能が特定の状況下でひっそりと（ユーザーに予測不可能な形で）無効化されないようにする
例：通知が出ていてもマップは常に「M」で開けるようにする

参考：

blog.nijibox.jp

www.uxpin.com

原則、オブジェクト指向のUIにする

❌️イマイチなところ：タスク指向のUI

例えばアーティア武器を強化するときのUIは

メニューから武器の強化（アクション・タスクの選択）を選ぶ
強化したい武器を選ぶ（オブジェクトの選択）

といった具合になっています。

更にいうと「生産」と「強化」と「解体」というアクションもそれぞれ別だし強化と解体は1階層深くにネストしているので、1つの同じ武器を生産して強化して解体したい場合（今作はこのシチュエーションに多く遭遇します）は

生産する
最初のメニューに戻って強化の画面に入る
強化する武器を選んで強化する
またメニューに戻って解体の画面に入る
解体する武器を選んで解体する

という多くのステップを踏むことになります。

⭕️気をつけたい点：まずオブジェクト指向のUIを検討する

※オブジェクト指向UIとは、ざっくりいうと操作する対象（オブジェクト）をまず選んで、それからタスク（アクション）を選ぶようなUIです。例えばECサイトにおける「商品ページに行く → カートに入れる」みたいなUIです。対義語がタスク指向UIです。

✅ ユーザーが対象（武器・防具など）にすぐアクセスできるようにする
✅ アクションはそのオブジェクトの文脈で選べるのが理想
⚠️ ただし常にオブジェクト指向がいいわけでもない
例：武器をまず一覧で選んで、そこから強化・解体などを選べる導線にする

参考：

blog.nijibox.jp

繰り返し発生する操作には「一括操作ボタン」をつける

❌️イマイチなところ：一括受け取りボタンが足りない

モンハンは素材や薬など様々な消費アイテムが存在し、定期的に受け取れる or 購入できる機会が発生します。受け取らないと損なのでほとんどのプレイヤーは全部受け取ろうとすると思うのですが、一括受け取り / 全選択みたいなUIが無い箇所も多く、繰り返し操作が発生します。

例1：ナタの「素材採集依頼」メニューではNPCが集めてくれた全地域の素材を 一括受取するボタンがなく 、地域ごとに受け取る必要があります。しかも受け取り後は収集依頼アイテムの 設定変更画面に自動で遷移 します。常に設定を変更するとは限らないので受け取りだけしてくれればいいのに…。

例2：支援船のアイテムを一括購入あるいは一括選択するボタンがありません。そのため (1) アイテムを選ぶ、(2) 個数を選ぶ、 (3) 購入しますか？→はいを選ぶ、という操作を全部のアイテムについて繰り返す必要があります。

❌️イマイチなところ：ガチャを10連で引けない

ワイルズでは通常の武器より強い「アーティア武器」という武器のカテゴリがあり、生産して「復元強化」をするとランダムな能力が付くという いわゆる「ガチャ」のシステム になっています。

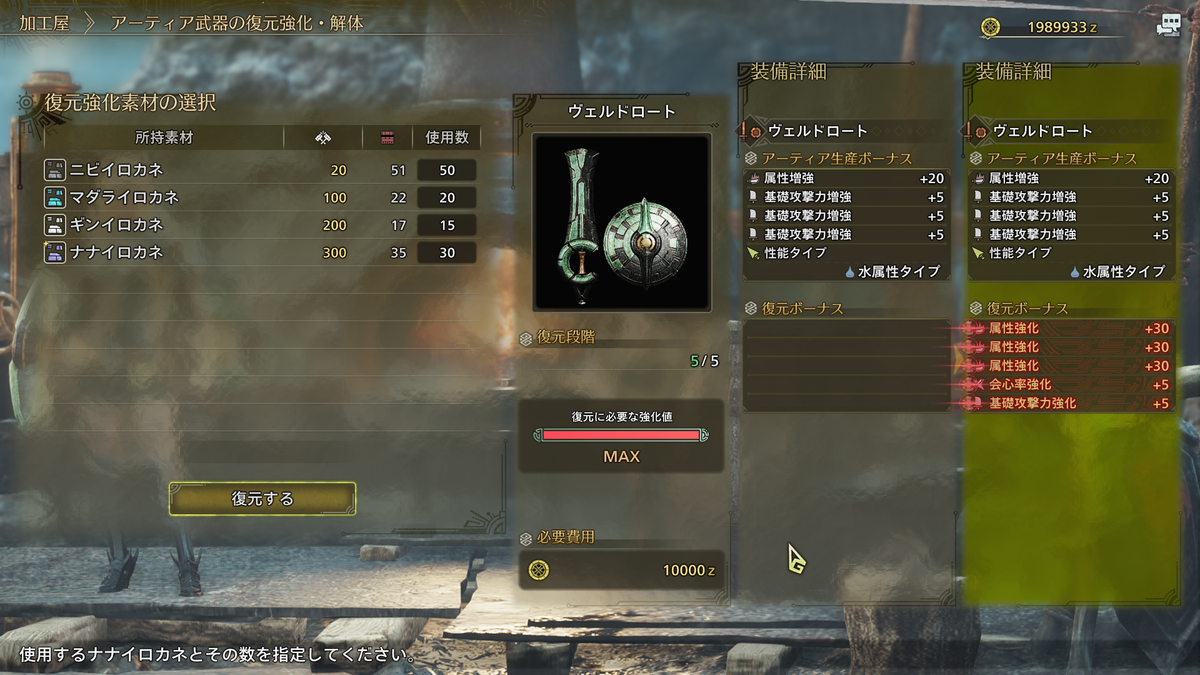
ガチャなので目当ての能力が付与された武器を偶然手にするまでは 何十回・何百回と武器の生産・強化・解体をしないといけないわけですが、現状は1本ずつしか生産・強化・解体ができません 。また生産は素材の組み合わせを考えて3つのパーツを選択して生産する必要がありますし、強化と解体もタスク指向UIのために操作が煩雑で、 ガチャを1回引くのに要する手間（操作回数）が多い 状態です。

多くの場合1タップでガチャを引けるソシャゲのガチャですら10個一括でガチャを引く「10連ガチャ」が用意されているにもかかわらずワイルズには10連がないため、主要なエンドコンテンツがとてもストレスフルなものになっています。

⭕️気をつけたい点：繰り返し発生する操作は一括操作機能など効率化できる機能をつける

✅ 繰り返しが発生するUIには一括操作機能を提供する
- 全選択、一括受け取りなど
「ユーザーにとって単調で退屈な繰り返し操作が発生していないか？」を考えてUIを設計する

まとめ

ワイルズを遊んでいて「自分がUIを作るときは気をつけたい」と思った点は次の3点になります：

1️⃣ 一貫性と予測可能性をもたせ、ユーザーに直感的な操作を可能とさせる

2️⃣ 原則、オブジェクト指向のUIにする

3️⃣ 繰り返し操作する必要がある箇所に一括操作ボタンを導入するなど、ユーザーの負担を減らす仕組みを検討する

また、1️⃣や3️⃣を考えるうえではユーザーの気持ちになって考えることが重要になってくるのかなと思います。ユースケースないしカスタマージャーニーについて深く思いを巡らせることが大事なのかなと思いました。

2025-04-29

LightGBM関連の過去記事まとめ

機械学習 Python

記事別のアクセス数を見るとLightGBM関連がやはり多いので過去に書いた記事へのリンク一覧みたいなのを置いておきます

論文について
- LightGBMについて
- 量子化学習について
ライブラリについて
- 欠損値の扱い
- その他

論文について

LightGBMについて

nigimitama.hatenablog.jp

LightGBMの論文「LightGBM: A Highly Efficient Gradient Boosting Decision Tree」について概要をまとめた記事です。

この論文内での新規性としては Gradient-based One-Side Sampling (GOSS) と Exclusive Feature Bundling (EFB) が提案されたことなのですが、ライブラリのlightgbmではデフォルトのハイパーパラメータの設定ではgossは使われてないんですよね。世間で高く評価されているライブラリとしてのlightgbmと論文は若干違う点に注意が必要です。

量子化学習について

nigimitama.hatenablog.jp

LightGBM論文の著者の一部が関わっている Quantized Training of Gradient Boosting Decision Trees という論文の概要について触れたのち、lightgbmを実際に動かして量子化の長短を確認した記事です。

ライブラリについて

欠損値の扱い

nigimitama.hatenablog.jp

欠損値を含むデータセットを雑に突っ込んでも動くのがlightgbmのいいところですが、どういう挙動なんだっけ？という確認をしたときのメモみたいな記事です。

その他

nigimitama.hatenablog.jp